题目内容
抛物线y=x2+x+p(p≠0)与x轴相交,其中一个交点的横坐标是p.那么该抛物线的顶点的坐标是( )
| A、(0,-2) | ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
分析:由于抛物线y=x2+x+p(p≠0)与x轴相交,其中一个交点的横坐标是p,所以把(p,0)代入解析式即可求出p,然后利用抛物线的顶点公式即可求出顶点坐标.
解答:解:∵抛物线y=x2+x+p(p≠0)与x轴相交,其中一个交点的横坐标是p,
∴把(p,0)代入解析式得0=p2+p+p,
∴p=-2或p=0,
而已知p≠0,
∴p=-2,
∴抛物线的解析式为y=x2+x-2
∴x=-
=-
,y=
=-
,
∴该抛物线的顶点的坐标是(-
,-
).
故选D.
∴把(p,0)代入解析式得0=p2+p+p,
∴p=-2或p=0,
而已知p≠0,
∴p=-2,
∴抛物线的解析式为y=x2+x-2
∴x=-
| b |
| 2a |
| 1 |
| 2 |
| 4ac-b2 |
| 4a |
| 9 |
| 4 |
∴该抛物线的顶点的坐标是(-
| 1 |
| 2 |
| 9 |
| 4 |
故选D.
点评:此题主要考查了利用与坐标轴交点确定抛物线的解析式和求抛物线顶点坐标,计算时要主要符号.

练习册系列答案
相关题目
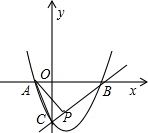 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点.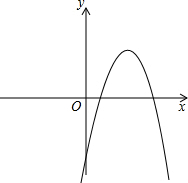 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4. 16、已知抛物线y=x2+bx+c的部分图象如图所示,若方程x2+bx+c=0有两个同号的实数根,则c的值可以是
16、已知抛物线y=x2+bx+c的部分图象如图所示,若方程x2+bx+c=0有两个同号的实数根,则c的值可以是