题目内容
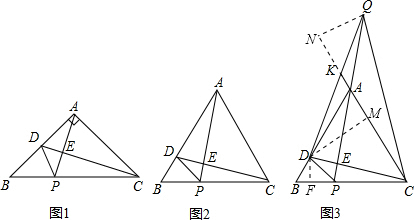
(2012•香坊区一模)已知:在△ABC中,AB=AC,点P是BC上一点,PC=2PB,连接AP,作∠APD=∠B交AB于点D.连接CD,交AP于点E.
(1)如图1,当∠BAC=90°时,则线段AD与BD的数量关系为
(2)如图2,当∠BAC=60°时,求证:AD=
BD;
(3)在(2)的条件下,过点C作∠DCQ=60°交PA的延长线于点Q如图3,连接DQ,延长CA交DQ于点K,若CQ=
.求线段AK的长.

(1)如图1,当∠BAC=90°时,则线段AD与BD的数量关系为
AD=
BD
| 5 |
| 4 |
AD=
BD
;| 5 |
| 4 |
(2)如图2,当∠BAC=60°时,求证:AD=
| 7 |
| 2 |
(3)在(2)的条件下,过点C作∠DCQ=60°交PA的延长线于点Q如图3,连接DQ,延长CA交DQ于点K,若CQ=
| ||
| 2 |

分析:(1)AD=
BD,理由为:如图1所示,由AB=AC及∠BAC=90°,得到三角形ABC为等腰直角三角形,可得出两个锐角为45°,再由∠APD=∠B,利用外角性质及角的加减,利用等量代换的思想得到∠BDP=∠APC,得出三角形PBD与三角形ACP相似,由相似得比例,设直角边AB=AC=3b,利用勾股定理表示出BC,再由PC=2PB,表示出BP和PC,再将表示的AC代入比例式,表示出BD,由AB-BD表示出AD,即可得出AD与BD的关系;
(2)如图2所示,由AB=AC及∠BAC=60°,得到三角形ABC为等边三角形,可得出∠B=∠BAC=∠ACB,且AB=AC=BC,由∠APD=∠B,利用外角性质及角的加减,利用等量代换的思想得到∠BDP=∠APC,得出三角形PBD与三角形ACP相似,由相似得比例,设三边上为3a,根据PC=2PB,表示出PC与BP,代入比例式中表示出BD,由AB-BD表示出AD,即可得出AD与BD的关系;
(3)过点D作DF⊥BC于F点,过D作DM⊥AC于M点,过Q作QN⊥CA交CA延长线于N点,如图3所示,由(2)表示出的AC,PB,PC,BD,AD,在直角三角形BFD中,由∠B=60°,得出∠BDF=30°,利用30°所对的直角边等于斜边的一半表示出BF,进而表示出DF,由BP-BF表示出PF,再由FP+PC表示出CF,在直角三角形CFD中,利用勾股定理表示出CD,由∠APD=∠B=60°,及∠DCQ=60°,得到∠APD=∠DCQ,再由一对对顶角相等,利用内角和定理推出∠PDE=∠CQE,由∠ACB=∠DCQ等号两边都减去∠ACD,得到∠PCD=∠ACQ,可得出三角形PCD与三角形ACQ相似,由相似得比例,根据CQ的长得出CD的长,确定出a的值,进而得出BD,AD,CF,DF的长,再由三角形FCD与三角形NCQ相似,由相似得比例,将已知的边代入求出CN与NQ的长,在直角三角形AMD中,由∠BAD=60°,得出∠ADM=30°,利用30°所对的直角边等于斜边的一半求出AM的长,进而得到DM的长,由AC-AM求出CM的长,再由CN-CM求出MN的长,由三角形DMK与三角形QNK相似,由相似得比例,得出KM与KN的比值,可得到KM与MN的比值,将MN的长代入求出KM的长,由KM-AM即可求出AK的长.
| 5 |
| 4 |
(2)如图2所示,由AB=AC及∠BAC=60°,得到三角形ABC为等边三角形,可得出∠B=∠BAC=∠ACB,且AB=AC=BC,由∠APD=∠B,利用外角性质及角的加减,利用等量代换的思想得到∠BDP=∠APC,得出三角形PBD与三角形ACP相似,由相似得比例,设三边上为3a,根据PC=2PB,表示出PC与BP,代入比例式中表示出BD,由AB-BD表示出AD,即可得出AD与BD的关系;
(3)过点D作DF⊥BC于F点,过D作DM⊥AC于M点,过Q作QN⊥CA交CA延长线于N点,如图3所示,由(2)表示出的AC,PB,PC,BD,AD,在直角三角形BFD中,由∠B=60°,得出∠BDF=30°,利用30°所对的直角边等于斜边的一半表示出BF,进而表示出DF,由BP-BF表示出PF,再由FP+PC表示出CF,在直角三角形CFD中,利用勾股定理表示出CD,由∠APD=∠B=60°,及∠DCQ=60°,得到∠APD=∠DCQ,再由一对对顶角相等,利用内角和定理推出∠PDE=∠CQE,由∠ACB=∠DCQ等号两边都减去∠ACD,得到∠PCD=∠ACQ,可得出三角形PCD与三角形ACQ相似,由相似得比例,根据CQ的长得出CD的长,确定出a的值,进而得出BD,AD,CF,DF的长,再由三角形FCD与三角形NCQ相似,由相似得比例,将已知的边代入求出CN与NQ的长,在直角三角形AMD中,由∠BAD=60°,得出∠ADM=30°,利用30°所对的直角边等于斜边的一半求出AM的长,进而得到DM的长,由AC-AM求出CM的长,再由CN-CM求出MN的长,由三角形DMK与三角形QNK相似,由相似得比例,得出KM与KN的比值,可得到KM与MN的比值,将MN的长代入求出KM的长,由KM-AM即可求出AK的长.
解答:(1)AD=
BD,理由为:
证明:∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
∴∠B=∠ACB=45°,
又∠CPD=∠B+∠BDP=∠APD+∠APC,且∠APD=∠B,
∴∠BDP=∠APC,
∴△PBD∽△ACP,
设AB=AC=3b,则有BC=3
b,
由PC=2PB,得到PB=
b,PC=2
b,
∴
=
,即
=
,
解得:BD=
b,
∴AD=AB-BD=3b-
b=
b,
则AD=
BD;
故答案为:AD=
BD.
(2)证明:∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴∠BAC=∠ACB=∠B=60°,AB=AC=BC,
设AB=AC=BC=3a,由PC=2PB,得到PB=a,PC=2a,
∵∠CPD=∠B+∠BDP=∠APD+∠APC,且∠APD=∠B,
∴∠BDP=∠APC,
∴△PBD∽△ACP,
∴
=
,即
=
,
∴BD=
a,
∴AD=AB-BD=3a-
a=
a,
∴AD=
BD;
(3)解:过点D作DF⊥BC于F点,过D作DM⊥AC于M点,过Q作QN⊥CA交CA延长线于N点,
由(2)知:AC=3a,PB=a,PC=2a,BD=
a,AD=
a,
在Rt△DFB中,∠B=60°,可得出∠BDF=30°,
∴BF=
BD=
a,DF=
a,
∴PF=PB-BF=
a,
∴CF=PF+PC=
a,
在Rt△CFD中,根据勾股定理得:CD2=CF2+DF2,
解得:CD=
a,
∵∠APD=∠B=60°,又∠DCQ=60°,
∴∠APD=∠DCQ,
∵∠PED=∠CEQ,
∴∠PDE=∠CQE,又∠ACB=60°,
∴∠ACB-∠ACD=∠DCQ-∠ACD,即∠PCD=∠ACQ,
∴△PCD∽△ACQ,
∴
=
=
=
,又CQ=
,
∴CD=
,即
a=
,
解得:a=1,
∴BD=
,AD=
,CF=
,DF=
,
∵∠CFD=∠CNQ=90°,∠FCD=∠NCQ,
∴△FCD∽△NCQ,
∴
=
=
,
∴CN=4,NQ=
,
∵在Rt△AMD中,∠DAM=60°,
∴∠BDF=30°,
∴AM=
,DM=
,
∴CM=AC-AM=
,
∴MN=CN-CM=
,
∵∠DMK=∠QNK=90°,∠DKM=∠QKN,
∴△DMK∽△QNK,
∴
=
=
,即KM=
KN,
∴KM=
MN=
×
=
,
则AK=KM-AM=
-
=
.
| 5 |
| 4 |
证明:∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
∴∠B=∠ACB=45°,
又∠CPD=∠B+∠BDP=∠APD+∠APC,且∠APD=∠B,
∴∠BDP=∠APC,
∴△PBD∽△ACP,
设AB=AC=3b,则有BC=3
| 2 |
由PC=2PB,得到PB=
| 2 |
| 2 |
∴
| BD |
| CP |
| PB |
| AC |
| BD | ||
2
|
| ||
| 3b |
解得:BD=
| 4 |
| 3 |
∴AD=AB-BD=3b-
| 4 |
| 3 |
| 5 |
| 3 |
则AD=
| 5 |
| 4 |
故答案为:AD=
| 5 |
| 4 |
(2)证明:∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴∠BAC=∠ACB=∠B=60°,AB=AC=BC,
设AB=AC=BC=3a,由PC=2PB,得到PB=a,PC=2a,
∵∠CPD=∠B+∠BDP=∠APD+∠APC,且∠APD=∠B,
∴∠BDP=∠APC,
∴△PBD∽△ACP,
∴
| BD |
| CP |
| PB |
| AC |
| BD |
| 2a |
| a |
| 3a |
∴BD=
| 2 |
| 3 |
∴AD=AB-BD=3a-
| 2 |
| 3 |
| 7 |
| 3 |
∴AD=
| 7 |
| 2 |
(3)解:过点D作DF⊥BC于F点,过D作DM⊥AC于M点,过Q作QN⊥CA交CA延长线于N点,

由(2)知:AC=3a,PB=a,PC=2a,BD=
| 2 |
| 3 |
| 7 |
| 3 |
在Rt△DFB中,∠B=60°,可得出∠BDF=30°,
∴BF=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
∴PF=PB-BF=
| 2 |
| 3 |
∴CF=PF+PC=
| 8 |
| 3 |
在Rt△CFD中,根据勾股定理得:CD2=CF2+DF2,
解得:CD=
| ||
| 3 |
∵∠APD=∠B=60°,又∠DCQ=60°,
∴∠APD=∠DCQ,
∵∠PED=∠CEQ,
∴∠PDE=∠CQE,又∠ACB=60°,
∴∠ACB-∠ACD=∠DCQ-∠ACD,即∠PCD=∠ACQ,
∴△PCD∽△ACQ,
∴
| CD |
| CQ |
| PC |
| CA |
| 2a |
| 3a |
| 2 |
| 3 |
| ||
| 2 |
∴CD=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
解得:a=1,
∴BD=
| 2 |
| 3 |
| 7 |
| 3 |
| 8 |
| 3 |
| ||
| 3 |
∵∠CFD=∠CNQ=90°,∠FCD=∠NCQ,
∴△FCD∽△NCQ,
∴
| DF |
| NQ |
| CF |
| CN |
| CD |
| CQ |
∴CN=4,NQ=
| ||
| 2 |
∵在Rt△AMD中,∠DAM=60°,
∴∠BDF=30°,
∴AM=
| 7 |
| 6 |
7
| ||
| 6 |
∴CM=AC-AM=
| 11 |
| 6 |
∴MN=CN-CM=
| 13 |
| 6 |
∵∠DMK=∠QNK=90°,∠DKM=∠QKN,
∴△DMK∽△QNK,
∴
| KM |
| KN |
| DM |
| QN |
| 7 |
| 3 |
| 7 |
| 3 |
∴KM=
| 7 |
| 10 |
| 7 |
| 10 |
| 13 |
| 6 |
| 91 |
| 60 |
则AK=KM-AM=
| 91 |
| 60 |
| 7 |
| 6 |
| 7 |
| 20 |
点评:此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,等腰直角三角形的判定与性质,等边三角形的判定与性质,含30°直角三角形的性质,利用了转化及等量代换的数学思想,是一道难道较强的压轴题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
