��Ŀ����
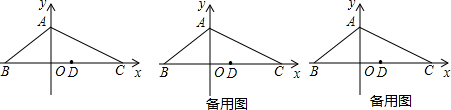
��2012•�㷻��һģ����ͼ����ƽ��ֱ������ϵ�У���0������ԭ�㣬�ڡ�ABC�У�BC=2AB����B������Ϊ��-4��0������D��BC���е㣬��tan��ACB=
��1�����A�����ꣻ
��2����P��C����������߶�CB��5����λ/����ٶ����յ�B�����˶�������P��PE��AB������ΪE��PE��ֱ��AC�ڵ�F����EF�ij�Ϊy��y��O������P���˶�ʱ��Ϊt�룬��y��t֮�ʵĺ�����ϵʽ��ֱ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����O����0Q��AC��AB��Q�㣬����DQ���Ƿ����������tֵ��ʹ��FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
| 1 | 2 |
��1�����A�����ꣻ
��2����P��C����������߶�CB��5����λ/����ٶ����յ�B�����˶�������P��PE��AB������ΪE��PE��ֱ��AC�ڵ�F����EF�ij�Ϊy��y��O������P���˶�ʱ��Ϊt�룬��y��t֮�ʵĺ�����ϵʽ��ֱ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����O����0Q��AC��AB��Q�㣬����DQ���Ƿ����������tֵ��ʹ��FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�

��������1����OA=a������tan��ACB=
���������к����Ķ���ó�OC=2a����BC=4+2a��AB=2+a��Ȼ����Rt��OAB�У��ɹ��ɶ����ó�AB2=OA2+OB2���г�����a�ķ��̣��ⷽ�����a��ֵ�����ɵõ�A�����ꣻ
��2������A��AG��AB����BC��G����Rt��GAB���ó�BG=
����CG=BC-BG=
�����������ó�0��t��2��t��
�����Է�����������ۣ���0��t��
�����ɡ�ABG�ס�EBP���ó�FP=6-3t-y�����ɡ�CFP�ס�CAG���ó�y=6-8t����
��t��2�����ɡ�ACG�ס�FCP���ó�PE=5t-y�����ɡ�BEP�ס�BAG���ó�y=8t-6��
��3��ͬ��2������������������ۣ��ٵ�0��t��
ʱ����Q��QM��OB��M����F��FN��BC��N������FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ����ڡ�FQD��90�㣬��ֻ�ܡ�QDF=90�㣮�ɡ�OBQ�ס�CBA���ó�BQ=2���ٽ�Rt��BQM���ó�QM=
��BM=
����DM=BD-BM=
���ɣ�2��֪FN=4t����CN=2FN=8t��DN=CD-CN=5-8t���������Ƕ�Ӧ��ȵ������������Ƶó���DNF�ס�QMD�������������ζ�Ӧ�߳ɱ����г�����ʽ�����t���ɣ��ڵ�
��t��2ʱ����Q��QM��OB��M����F��FN��BC��N��FG��QM��G������FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ����ڡ�FDQ��90�㣬��ֻ�ܡ�FQD=90�㣬�ɡ�FGQ�ס�QMD���������������ζ�Ӧ�߳ɱ����г�����ʽ�����t���ɣ�
| 1 |
| 2 |
��2������A��AG��AB����BC��G����Rt��GAB���ó�BG=
| 25 |
| 4 |
| 15 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
��3��ͬ��2������������������ۣ��ٵ�0��t��
| 3 |
| 4 |
| 6 |
| 5 |
| 8 |
| 5 |
| 17 |
| 5 |
| 3 |
| 4 |
����⣺��1����OA=a�����A�����꣨0��a����
��tan��ACB=
=
��
��OC=2OA=2a��
��BC=OB+OC=4+2a��
��BC=2AB��
��AB=2+a��
��Rt��OAB�У��ߡ�AOB=90�㣬
��AB2=OA2+OB2������a+2��2=a2+42��
���a=3��
��A��0��3����
 ��2������A��AG��AB����BC��G��
��2������A��AG��AB����BC��G��
��Rt��GAB�У��ߡ�GAB=90�㣬
��AG=AB•tan��B=5��
=
��
BG=
=
=
��
��CG=BC-BG=10-
=
��
�ߵ�P��C����������߶�CB��5����λ/����ٶ����յ�B�����˶�����P���˶�ʱ��Ϊt�룬
��0��5t��10��
��0��t��2��
��P��G�غ�ʱ��E��F��A�����غϣ���ʱEF�ij�y=0������֪ì�ܣ�
��t��
=
=
��
������������ۣ�
 �ٵ�0��t��
�ٵ�0��t��
ʱ����ͼ2��
��AG��EP��
���ABG�ס�EBP��
��
=
��
=
��
���FP=6-3t-y��
��FP��AG��
���CFP�ס�CAG��
��
=
��
��AG=CG=
��
��FP=PC����6-3t-y=5t��
��y=6-8t��
 �ڵ�
�ڵ�
��t��2ʱ����ͼ3��
��AG��FP��
���ACG�ס�FCP��
��
=
��
��AG=CG=
��
��FP=CP����y+PE=5t��
��PE=5t-y��
��PE��AG��
���BEP�ס�BAG��
��
=
��
=
��
��y=8t-6��
����������y=
��
 ��3��������������ۣ�
��3��������������ۣ�
�ٵ�0��t��
ʱ����Q��QM��OB��M����F��FN��BC��N����ͼ4��
����FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ��ߡ�FQD����AQD����AQO=��EAC��90�㣬
���QDF=90�㣮
��OQ��AC��
���OBQ�ס�CBA��
��
=
����
=
��
��BQ=2��
��Rt��BQM�У�QM=BQ•sin��B=2��
=
��BM=BQ•cos��B=2��
=
��
��DM=BD-BM=5-
=
��
�ɣ�2��֪FN=FP•sin��FPN=CP•sin��OAB=5t•
=4t��
��CN=2FN=8t��DN=CD-CN=5-8t��
�ߡ�FND=��DMQ=90�㣬��FDN=��DQM=90��-��QDM��
���DNF�ס�QMD��
��
=
��
��
=
��
���t=
��
 �ڵ�
�ڵ�
��t��2ʱ����Q��QM��OB��M����F��FN��BC��N��FG��QM��G����ͼ5��
����FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ��ߡ�FDQ����ADQ����ADB��90�㣬
���FQD=90�㣮
��GM=FN=4t��
��GQ=GM-QM=4t-
��GF=MN=BC-BM-CN=10-
-8t=
-8t��
�ߡ�FGQ=��QMD=90�㣬��FQG=��QDM=90��-��DQM��
���FGQ�ס�QMD��
��
=
��
��
=
��
���t=
��
������������t=
��t=
ʱ����FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ�
��tan��ACB=
| OA |
| OC |
| 1 |
| 2 |
��OC=2OA=2a��
��BC=OB+OC=4+2a��
��BC=2AB��
��AB=2+a��
��Rt��OAB�У��ߡ�AOB=90�㣬
��AB2=OA2+OB2������a+2��2=a2+42��
���a=3��
��A��0��3����
 ��2������A��AG��AB����BC��G��
��2������A��AG��AB����BC��G����Rt��GAB�У��ߡ�GAB=90�㣬
��AG=AB•tan��B=5��
| 3 |
| 4 |
| 15 |
| 4 |
BG=
| AB |
| cos��B |
| 5 | ||
|
| 25 |
| 4 |
��CG=BC-BG=10-
| 25 |
| 4 |
| 15 |
| 4 |
�ߵ�P��C����������߶�CB��5����λ/����ٶ����յ�B�����˶�����P���˶�ʱ��Ϊt�룬
��0��5t��10��
��0��t��2��
��P��G�غ�ʱ��E��F��A�����غϣ���ʱEF�ij�y=0������֪ì�ܣ�
��t��
| CG |
| 5 |
| ||
| 5 |
| 3 |
| 4 |
������������ۣ�
 �ٵ�0��t��
�ٵ�0��t��| 3 |
| 4 |
��AG��EP��
���ABG�ס�EBP��
��
| AG |
| EP |
| BG |
| BP |
| ||
| y+FP |
| ||
| 10-5t |
���FP=6-3t-y��
��FP��AG��
���CFP�ס�CAG��
��
| FP |
| AG |
| PC |
| CG |
��AG=CG=
| 15 |
| 4 |
��FP=PC����6-3t-y=5t��
��y=6-8t��
 �ڵ�
�ڵ�| 3 |
| 4 |
��AG��FP��
���ACG�ס�FCP��
��
| AG |
| FP |
| CG |
| CP |
��AG=CG=
| 15 |
| 4 |
��FP=CP����y+PE=5t��
��PE=5t-y��
��PE��AG��
���BEP�ס�BAG��
��
| PE |
| AG |
| BP |
| BG |
| 5t-y | ||
|
| 10-5t | ||
|
��y=8t-6��
����������y=
|
 ��3��������������ۣ�
��3��������������ۣ��ٵ�0��t��
| 3 |
| 4 |
����FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ��ߡ�FQD����AQD����AQO=��EAC��90�㣬
���QDF=90�㣮
��OQ��AC��
���OBQ�ס�CBA��
��
| BQ |
| BA |
| BO |
| BC |
| BQ |
| 5 |
| 4 |
| 10 |
��BQ=2��
��Rt��BQM�У�QM=BQ•sin��B=2��
| 3 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
��DM=BD-BM=5-
| 8 |
| 5 |
| 17 |
| 5 |
�ɣ�2��֪FN=FP•sin��FPN=CP•sin��OAB=5t•
| 4 |
| 5 |
��CN=2FN=8t��DN=CD-CN=5-8t��
�ߡ�FND=��DMQ=90�㣬��FDN=��DQM=90��-��QDM��
���DNF�ס�QMD��
��
| DN |
| QM |
| FN |
| DM |
��
| 5-8t | ||
|
| 4t | ||
|
���t=
| 17 |
| 32 |
 �ڵ�
�ڵ�| 3 |
| 4 |
����FDQ����DQΪһ��ֱ�DZߵ�ֱ�������Σ��ߡ�FDQ����ADQ����ADB��90�㣬
���FQD=90�㣮
��GM=FN=4t��
��GQ=GM-QM=4t-
| 6 |
| 5 |
| 8 |
| 5 |
| 42 |
| 5 |
�ߡ�FGQ=��QMD=90�㣬��FQG=��QDM=90��-��DQM��
���FGQ�ס�QMD��
��
| FG |
| QM |
| GQ |
| MD |
��
| ||
|
4t-
| ||
|
���t=
| 15 |
| 16 |
������������t=
| 17 |
| 32 |
| 15 |
| 16 |
������������Ҫ������������Ǻ����Ķ��壬���ɶ�������ֱ�������Σ����������ε��ж������ʵ�֪ʶ���ۺ��Խ�ǿ���ѶȽϴ��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ