题目内容
某饮料厂现有A、B两种果汁原料至多分别有19千克和17.2千克,准备配制甲、乙两种新型饮料共50瓶。表中是试验的有关数据:
⑴ 假设甲种饮料需要配制x瓶,请写出满足条件的不等式组
⑵ 通过计算说明有哪几种配制方案
⑶ 设甲种饮料每瓶成本为4元,乙种饮料每瓶成本为3元,这两种饮料的成本总额为y元,通过计算说明,当甲种饮料配制多少瓶时,甲、乙两种饮料的总成本最少?
| 饮料 每瓶新型 饮料含果汁量 | 甲种 新型饮料 | 乙种 新型饮料 |
| A种果汁(单位:千克) | 0.5 | 0.2 |
| B种果汁(单位:千克) | 0.3 | 0.4 |
⑵ 通过计算说明有哪几种配制方案
⑶ 设甲种饮料每瓶成本为4元,乙种饮料每瓶成本为3元,这两种饮料的成本总额为y元,通过计算说明,当甲种饮料配制多少瓶时,甲、乙两种饮料的总成本最少?
⑴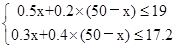 ⑵有三种配制方案:
⑵有三种配制方案:
方案一:配制甲种饮料28瓶;配制乙种饮料22瓶
方案二:配制甲种饮料29瓶;配制乙种饮料21瓶
方案三:配制甲种饮料30瓶;配制乙种饮料20瓶
⑶当甲种饮料配制28瓶时,甲、乙两种饮料的总成本最少
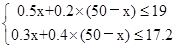 ⑵有三种配制方案:
⑵有三种配制方案:方案一:配制甲种饮料28瓶;配制乙种饮料22瓶
方案二:配制甲种饮料29瓶;配制乙种饮料21瓶
方案三:配制甲种饮料30瓶;配制乙种饮料20瓶
⑶当甲种饮料配制28瓶时,甲、乙两种饮料的总成本最少
试题分析:⑴依题意知甲种饮料需要配制x瓶,总共甲乙有50瓶,故乙表示为50-x瓶。由图表中可知,甲种饮料含A果汁0.5kg,含B果汁0.3kg。所以分别表示为0.5x和0.3x。同理可知乙种饮料中含A果汁0.2(50-x)kg,含B果汁0.4(50-x)。根据A、B两种果汁原料至多分别有19千克和17.2千克,列式得:
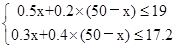
⑵
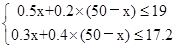 解得28≤x≤30,又x为整数,所以x的值为28、29和30. 50-x的值为22、21、和20
解得28≤x≤30,又x为整数,所以x的值为28、29和30. 50-x的值为22、21、和20所以有三种配制方案:
方案一:配制甲种饮料28瓶;配制乙种饮料22瓶
方案二:配制甲种饮料29瓶;配制乙种饮料21瓶
方案三:配制甲种饮料30瓶;配制乙种饮料20瓶
⑶由题意有y=4x+3(50-x)=x+150
由此可知y随x的增大而增大,所以, 当x=28时,y最小
即当甲种饮料配制28瓶时,甲、乙两种饮料的总成本最少.
点评:本题难度中等,主要考查学生对不等式组知识点的掌握与解决实际问题运用能力。为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 的解集是【 】
的解集是【 】 ,求满足条件的所有正整数x.
,求满足条件的所有正整数x. ;(2)
;(2)
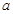 >b,得
>b,得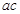 >
>
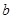 ,得
,得
 ,得
,得

 无解,那么m的取值范围是( )
无解,那么m的取值范围是( ) 的最小整数解为
的最小整数解为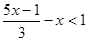 ,并将解集在数轴上表示出来,写出它的正整数解.
,并将解集在数轴上表示出来,写出它的正整数解.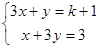 的解为x,y,且x+y>0,则k的范围是
的解为x,y,且x+y>0,则k的范围是