题目内容
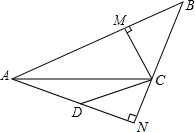 如图,AC平分∠BAD,CM⊥AB于点M,CN⊥AN,且BM=DN,则∠ADC与∠ABC的关系是
如图,AC平分∠BAD,CM⊥AB于点M,CN⊥AN,且BM=DN,则∠ADC与∠ABC的关系是
- A.相等
- B.互补
- C.和为150°
- D.和为165°
B
分析:先根据全等三角形的判定定理得出△CND≌△CMB,由全等三角形的性质可知∠ABC=∠CDN,故可得出结论.
解答:∵AC平分∠BAD,CM⊥AB于点M,CN⊥AN,
∴CM=CN,∠CND=∠BMC=90°,
∵BM=DN,
在△CND与△CMB中,
∵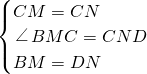 ,
,
∴△CND≌△CMB,
∴∠B=∠CDN,
∵∠CDN+∠ADC=180°,
∴∠ADC+∠ABC=180°.
故选B.
点评:本题考查的是角平分线的性质及全等三角形的判定与性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.
分析:先根据全等三角形的判定定理得出△CND≌△CMB,由全等三角形的性质可知∠ABC=∠CDN,故可得出结论.
解答:∵AC平分∠BAD,CM⊥AB于点M,CN⊥AN,
∴CM=CN,∠CND=∠BMC=90°,
∵BM=DN,
在△CND与△CMB中,
∵
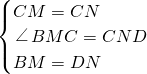 ,
,∴△CND≌△CMB,
∴∠B=∠CDN,
∵∠CDN+∠ADC=180°,
∴∠ADC+∠ABC=180°.
故选B.
点评:本题考查的是角平分线的性质及全等三角形的判定与性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
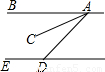
 (2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是
(2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )