Question

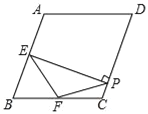
【题目】如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（　　）

A. 50° B. 55° C. 60° D. 45°

Answer 1

【答案】A

【解析】首先延长PF交AB的延长线于点G．根据已知可得∠B，∠BEF，∠BFE的度数，再根据余角的性质可得到∠EPF的度数，从而不难求得∠FPC的度数．

【解答】解：延长PF交AB的延长线于点G．如图所示：

在△BGF与△CPF中，∠GBF=∠PCF，BF=CF，∠BFG=∠CFG，，

∴△BGF≌△CPF（ASA），

∴GF=PF，

∴F为PG中点．

又∵由题可知，∠BEP=90°，

∴EF=PG，

∵PF=PG，

∴EF=PF，

∴∠FEP=∠EPF，

∵∠BEP=∠EPC=90°，

∴∠BEP﹣∠FEP=∠EPC﹣∠EPF，即∠BEF=∠FPC，

∵四边形ABCD为菱形，

∴AB=BC，∠ABC=180°﹣∠A=80°，

∵E，F分别为AB，BC的中点，

∴BE=BF，∠BEF=∠BFE==50°，

∴∠FPC=50°；

故选A．

“点睛”此题主要考查了菱形的性质的理解及运用，灵活应用菱形的性质是解决问题的关键．