题目内容
【题目】对某一个函数给出如下定义:如果存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,那么称这个函数是有上界函数,在所有满足条件的
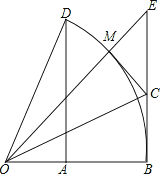
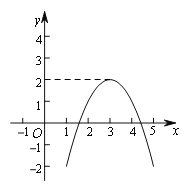
,那么称这个函数是有上界函数,在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
中,其最小值称为这个函数的上确界.例如下图中的函数是有上界函数,其上确界是2.
(1)分别判断函数![]() (
(![]() )和
)和![]() (
(![]() )是不是有上界函数?如果是有上界函数,求其上确界;
)是不是有上界函数?如果是有上界函数,求其上确界;
(2)如果函数![]() (
(![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过
,且这个函数的最小值不超过![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若函数![]() (
(![]() )是以3为上确界的有上界函数,求
)是以3为上确界的有上界函数,求![]() 值.
值.
【答案】(1)y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;(2)-1≤a<1;(3)![]() .
.
【解析】
试题分析:(1)根据有界函数函数的定义和上确界定义分析即可;
(2)根据函数的上确界和函数增减性得到2-a=b,函数的最小值为2-b,根据b>a,函数的最小值不超过2a+1,列不等式求解集即可;
(3)根据对称轴方程x=a和上确界为3,分类讨论a≤3时和a>3时,列方程求解.
试题解析:(1)根据有界函数定义,y=![]() (x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(x<0)不是有上界函数;y=2x-3(x<2)是有上界函数,上确界是1;
(2)∵在y=-x+2中,y随x的增大而减小,
∴上确界为2-a,即2-a=b,
又b>a,所以2-a>a,解得a<1,
∵函数的最小值是2-b,∴2-b≤2a+1,得a≤2a+1,解得a≥-1,
综上所述:-1≤a<1;
(3)函数的对称轴为x=a,
①当a≤3时,函数的上确界是25-10a+2=27-10a,
∴27-10a=3,解得a=![]() ,符合题意;
,符合题意;
②当a>3时,函数的上确界是1-2a+2=3-2a,
∴3-2a=3,解得a=0,不符合题意.
综上所述:a=![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目