题目内容
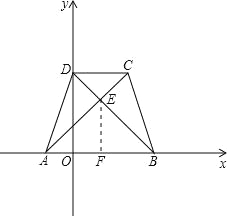
【题目】在平面直角坐标系中,已知等腰梯形ABCD的三个顶点A(-2,0),B(6,0),C(4,6),对角线AC与BD相交于点E.
(1)求E的坐标;
(2)若M是x轴上一动点,求MC+MD的最小值;
(3)在y轴正半轴上求点P,使以P、B、C为顶点的三角形为等腰三角形.

【答案】(1) 点E的坐标为(2,4);(2) ![]() ;(3) 点P的坐标为:(0,6+
;(3) 点P的坐标为:(0,6+![]() ),(0,6-
),(0,6-![]() ),(0,2),(0,
),(0,2),(0,![]() ).
).
【解析】
试题分析:(1)作EF⊥AB,根据已知,可得出OD=6,FB=4,OF=2,然后,根据相似,即可求出EF的长,即可得出点E的坐标;
(2)作点D关于x轴的对称点D′,则D′的坐标为(0,-6),根据两点间的距离公式,算出即可;
(3)设点P(0,y),y>0,分三种情况,①PC=BC;②PB=BC;③PB=PC;解答出即可;
试题解析:(1)作EF⊥AB,
∴![]() ,
,
∵梯形ABCD是等腰梯形,
∴AE=BE,
∴在等腰三角形ABE中,AF=BF,
∵A(-2,0),B(6,0),C(4,6),
∴点D的坐标为(0,6),
∴OD=6,FB=4,OF=2,
∴![]() ,
,
∴EF=4,
∴点E的坐标为(2,4);
(2)由题意可得,
点D关于x轴的对称点D′的坐标为(0,-6),
CD′与x轴的交点为M,
∴此时,MC+MD=CD′为最小值,
∴CD′=![]() ;
;
(3)设点P(0,y),y>0,
分三种情况,①PC=BC;
∴42+(6-y)2=22+62,
解得,y=6±![]() ;
;
②PB=BC;
∴62+y2=22+62,
解得,y=2,y=-2(舍去);
③PB=PC;
∴62+y2=42+(6-y)2,
解得,y=![]() ;
;
综上,点P的坐标为:(0,6+![]() ),(0,6-
),(0,6-![]() ),(0,2),(0,
),(0,2),(0,![]() ).
).

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目




