Question

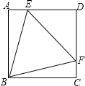
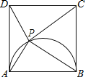
【题目】如图，已知四边形是边长为的正方形，以为直径向正方形内作半圆，为半圆上一动点（不与、重合），当________时，为等腰三角形．

Answer 1

【答案】或或

【解析】

分别从当PA=PD，PA=AD，AD=PD时，△PAD是等腰三角形讨论，然后由等腰三角形的性质与射影定理即可求得答案.

解：①当PA=PD时，

此时P位于四边形ABCD的中心，

过点P作PE⊥AD于E，作PM⊥AB于M，

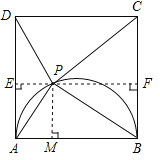
则四边形EAMP是正方形，

∴PM=PE=AB=2，

∵PM2=AMBM=4，

∵AM+BM=4，

∴AM=2，

∴PA=2，

②当PA=AD时，PA=4（舍）；

③当PD=DA时，以点D为圆心，DA为半径作圆与弧AB的交点为点P．

连PD，令AB中点为O，再连DO，PO，DO交AP于点G，

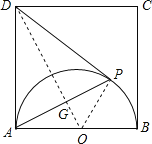
则△ADO≌△PDO，

∴DO⊥AP，AG=PG，

∴AP=2AG，

又∵DA=2AO，

∴AG=2OG，

设AG为2x，OG为x，

∴（2x）2+x2=4，

∴x=，

∴AG=2x=，

∴PA=2AG=；

∴PA=2或4或，

故答案为：2或4或.