题目内容
若x1和x2分别是一元二次方程2x2+7x-4=0的两根.
(1)求|x1-x2|的值; (2)x13+x23.
(1)求|x1-x2|的值; (2)x13+x23.
分析:(1)先利用根与系数的关系得到两根之和及两根之差,再对要求的代数式变形,把数值代入求解即可;
(2)利用立方和公式把代数式因式分解,再变形.再利用根与系数的关系即可求解.
(2)利用立方和公式把代数式因式分解,再变形.再利用根与系数的关系即可求解.
解答:解:(1)∵x1和x2分别是一元二次方程2x2+7x-4=0的两根.
∴x1+x2=-
=-
,x1•x2=
=-2,
∵|x1-x2|=
=
(2)∵x13+x23=(x1+x2)(x12-x1x2+x22)
=(x1+x2)[(x1+x2)2-3x1x2]
∵x1+x2=-
=-
,x1•x2=
=-2,
∴原式=-
.
∴x1+x2=-
| b |
| a |
| 7 |
| 2 |
| c |
| a |
∵|x1-x2|=
| (x1+x2) 2-4x 1•x 2 |
| 9 |
| 2 |
(2)∵x13+x23=(x1+x2)(x12-x1x2+x22)
=(x1+x2)[(x1+x2)2-3x1x2]
∵x1+x2=-
| b |
| a |
| 7 |
| 2 |
| c |
| a |
∴原式=-
| 511 |
| 8 |
点评:本题考查了根与系数的关系,常用根与系数的关系解决以下问题:①不解方程,判断两个数是不是一元二次方程的两个根.②已知方程及方程的一个根,求另一个根及未知数.③不解方程求关于根的式子的值,如求,x12+x22等等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
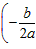 ,
,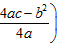 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线。
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线。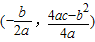 ,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线. ,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.