Question

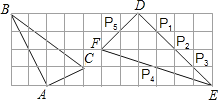
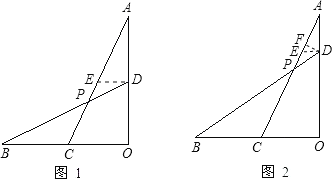
【题目】已知线段OA⊥OB，C为OB上中点，D为AO上一点，连AC、BD交于P点．

（1）如图1，当OA=OB且D为AO中点时，求的值；

（2）如图2，当OA=OB，时，求tan∠BPC．

Answer 1

【答案】（1）2；（2）．

【解析】

试题分析：（1）过D作BO的平行线，根据平行线分线段成比例定理，在△ACO中ED：CO=AD：AO，在△ADE和△PCB中，ED：BC=PE：PC，再根据C是BO的中点，可以求出PE：PC=1：2，再根据三角形中位线定理，E是AC的中点，利用比例变形求出AP与PC的比值等于2；

（2）同（1）的方法，先求出PC=AC，再过D作DF⊥AC于F，设AD为a，利用勾股定理求出AC等于2 a，再利用相似三角形对应边成比例求出DF、AF的值，而PF=AC﹣AF﹣PC，也可求出，又∠BPC与∠FPD是对顶角，所以其正切值便可求出．

解：（1）过D作DE∥CO交AC于E，

∵D为OA中点，∴AE=CE=，，

∵点C为OB中点，

∴BC=CO，，

∴，

∴PC==，

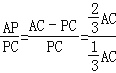∴=2；

（2）过点D作DE∥BO交AC于E，

∵，∴==，

∵点C为OB中点，∴，

∴，∴PC==，

过D作DF⊥AC，垂足为F，设AD=a，则AO=4a，

∵OA=OB，点C为OB中点，∴CO=2a，

在Rt△ACO中，AC===2 a，

又∵Rt△ADF∽Rt△ACO，∴，

∴AF=，DF=，

PF=AC﹣AF﹣PC=2 a﹣﹣=，

tan∠BPC=tan∠FPD==．