题目内容
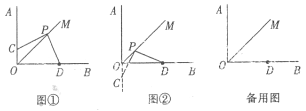
【题目】已知一次函数y=-![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
【答案】(1)B(8,0);(2)直线AE的表达式为y=-2x+6; (3) △OFB为等腰三角形,S△OBF=8.
【解析】试题分析:(1)对于一次函数y=-![]() x+6,令y=0和x=0求出对应的x与y的值,确定出OA及OB的长,即可确定出B的坐标;
x+6,令y=0和x=0求出对应的x与y的值,确定出OA及OB的长,即可确定出B的坐标;
(2)由(1)得出A的坐标,利用勾股定理求出AB的长,过E作EG垂直于AB,由AE为角平分线,利用角平分线定理得到EO=EG,利用HL可得出直角三角形AOE与直角三角形AGE全等,可得出AO=AG,设OE=EG=x,由OB-OE表示出EB,由AB-AG=AB-AO表示出BG,在直角三角形BEG中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出OE的长,得出E的坐标,设直线AE的解析式为y=kx+b(k≠0),将A和E的坐标代入,得到关于k与b的方程组,求出方程组的解得到k与b的值,即可得到直线AE的解析式;
(3)延长BF与y轴交于K点,由AF为角平分线得到一对角相等,再由AF与BF垂直得到一对直角相等,以及AF为公共边,利用ASA得出三角形AKF与三角形ABF全等,可得出AK=AB,利用三线合一得到F为BK的中点,在直角三角形OBK中,利用斜边上的中线等于斜边的一半得到OF为BK的一半,即OF=BF,过F作FH垂直于x轴于H点,利用三线合一得到H为OB的中点,由OB的长求出OH的长,即为F的横坐标,将求出的横坐标代入直线AE解析式中求出对应的纵坐标,即为HF的长,以OB为底,FH为高,利用三角形的面积公式即可求出三角形BOF的面积;
试题解析:(1)对于y=- ![]() x+6,
x+6,
当x=0时,y=6;当y=0时,x=8,
∴OA=6,OB=8,
在Rt△AOB中,根据勾股定理得:AB=10,
则A(0,6),B(8,0);
(2)过点E作EG⊥AB,垂足为G
∵AE平分∠BAO,EO⊥AO,EG⊥AG,
∴EG=OE,
在Rt△AOE和Rt△AGE中, ![]()
∴Rt△AOE≌Rt△AGE(HL),
∴AG=AO,
设OE=EG=x,则有BE=8-x,BG=AB-AG=10-6=4,
在Rt△BEG中,EG=x,BG=4,BE=8-x,
根据勾股定理得:x2+42=(8-x)2,
解得:x=3,
∴E(3,0),
设直线AE的表达式为y=kx+b(k≠0),
将A(0,6),E(3,0)代入y=kx+b得: ![]() ,解得
,解得![]()
则直线AE的表达式为y=-2x+6;
(3)延长BF交y轴于点K,
∵AE平分∠BAO,
∴∠KAF=∠BAF,
又BF⊥AE,
∴∠AFK=∠AFB=90°
∵AF=AF
∴△AFK≌△AFB,
∴FK=FB,即F为KB的中点,
又∵△BOK为直角三角形,
∴OF= ![]() BK=BF,
BK=BF,
∴△OFB为等腰三角形,
过点F作FH⊥OB,垂足为H(如图2所示),
∵OF=BF,FH⊥OB,
∴OH=BH=4,
∴F点的横坐标为4,
设F(4,y),将F(4,y)代入y=-2x+6,得:y=-2,
FH=|-2|=2,
则S△OBF= ![]() OBFH=
OBFH=![]() ×8×2=8;
×8×2=8;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案