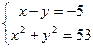题目内容
已知关于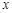 的方程
的方程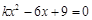 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 .
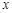 的方程
的方程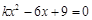 有两个不相等的实数根,则k的取值范围是 .
有两个不相等的实数根,则k的取值范围是 .k﹤1且k≠0
因为关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根,所以根的判别式△=b2-4ac>0,建立关于k的不等式,解得k的取值范围,还要考虑二次项系数不为0.=36-36k>0,即k<1,且k≠0.
解:∵方程有两个不相等的实数根,
∴△=b2-4ac.=36-36k>0,即k<1,且k≠0.
那么实数k的取值范围是k<1且k≠0.
本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解:∵方程有两个不相等的实数根,
∴△=b2-4ac.=36-36k>0,即k<1,且k≠0.
那么实数k的取值范围是k<1且k≠0.
本题考查了一元二次方程根的判别式的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目


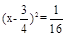

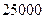 元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米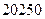 元的均价开盘销售.
元的均价开盘销售.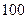 平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月
平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月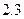 元/米2.请问哪种方案更优惠?
元/米2.请问哪种方案更优惠?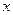 的方程
的方程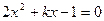 一个根是-1,求
一个根是-1,求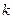 值及另一个根.
值及另一个根.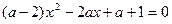 没有实数根,求
没有实数根,求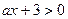 的解集(用含
的解集(用含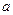 的式子表示)
的式子表示) 的一个根为
的一个根为 ,则
,则
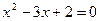 (2)
(2)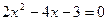
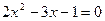 (4)
(4)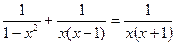
 (6)
(6)