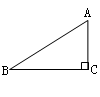
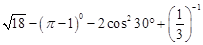题目内容
在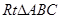 中,
中,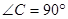 ,
,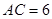 ,
,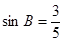 ,⊙
,⊙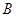 的半径长为1,⊙
的半径长为1,⊙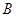 交边
交边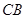 于点
于点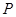 ,
,
点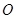 是边
是边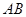 上的动点.
上的动点.
(1)如图1,将⊙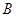 绕点
绕点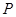 旋转
旋转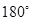 得到⊙
得到⊙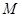 ,请判断⊙
,请判断⊙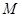 与直线
与直线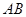 的位置关系;(4分)
的位置关系;(4分)
(2)如图2,在(1)的条件下,当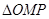 是等腰三角形时,求
是等腰三角形时,求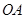 的长; (5分)
的长; (5分)
(3)如图3,点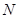 是边
是边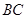 上的动点,如果以
上的动点,如果以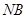 为半径的⊙
为半径的⊙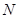 和以
和以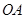 为半径的⊙
为半径的⊙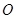 外切,设
外切,设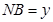 ,
,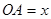 ,求
,求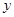 关于
关于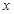 的函数关系式及定义域.(5分).
的函数关系式及定义域.(5分).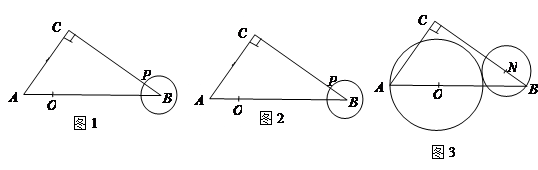
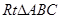 中,
中,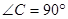 ,
,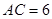 ,
,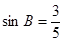 ,⊙
,⊙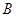 的半径长为1,⊙
的半径长为1,⊙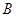 交边
交边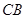 于点
于点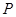 ,
,点
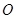 是边
是边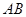 上的动点.
上的动点.(1)如图1,将⊙
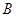 绕点
绕点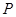 旋转
旋转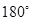 得到⊙
得到⊙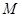 ,请判断⊙
,请判断⊙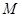 与直线
与直线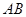 的位置关系;(4分)
的位置关系;(4分)(2)如图2,在(1)的条件下,当
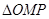 是等腰三角形时,求
是等腰三角形时,求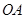 的长; (5分)
的长; (5分)(3)如图3,点
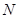 是边
是边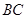 上的动点,如果以
上的动点,如果以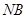 为半径的⊙
为半径的⊙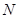 和以
和以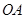 为半径的⊙
为半径的⊙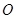 外切,设
外切,设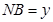 ,
,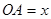 ,求
,求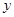 关于
关于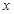 的函数关系式及定义域.(5分).
的函数关系式及定义域.(5分).
(1)⊙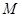 与直线
与直线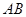 相离(2)
相离(2) 或
或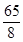 .(3)
.(3)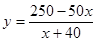 ,定义域为:
,定义域为: <
<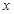 <
<
 与直线
与直线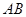 相离(2)
相离(2) 或
或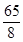 .(3)
.(3)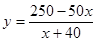 ,定义域为:
,定义域为: <
<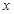 <
<
解:(1)在Rt△ABC中,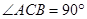 ,
,
∵ ,
,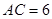
∴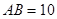 ,
, (1分)
(1分)
过点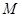 作
作 ,垂足为
,垂足为 . (1分)
. (1分)
在 中,
中,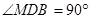 ,∴
,∴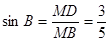 ,
,
∵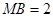 ,
,
∴ >
>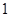 (1分)
(1分)
∴⊙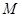 与直线
与直线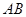 相离. (1分)
相离. (1分)
解:(2)分三种情况:
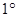 ∵
∵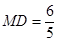 >
>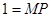 ,
,
∴ >
>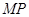 ; (1分)
; (1分)
 当
当 时,易得
时,易得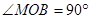 ,
,
∴ ,
,
∴ ,
,
∴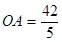 ; (2分)
; (2分)
 当
当 时,过点
时,过点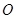 作
作 ,垂足为
,垂足为 .
.
∴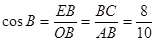 ,
,
∴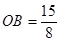 ,
,
∴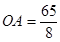 . (2分)
. (2分)
综合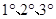 ,当
,当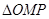 是等腰三角形时,
是等腰三角形时,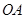 的长为
的长为 或
或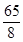 .
.
解:(3)联结 ,过点
,过点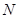 作
作 ,垂足为
,垂足为 .
.
在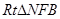 中,
中,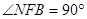 ,
,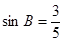 ,
,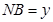 ;
;
∴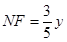 ,
, ;
;
∴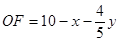 , (1分)
, (1分)
∵⊙ 和⊙
和⊙ 外切,
外切,
∴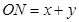 ; (1分)
; (1分)
在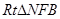 中,
中,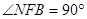 ,
,
∴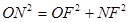 ;
;
即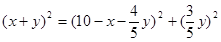 ;
;
∴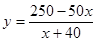 ; (2分)
; (2分)
定义域为: <
<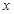 <
< .
.
(1)过点M作MD⊥AB,垂足为D,根据MB=2,结合sin∠B的值,可得出MD的长,与圆M的半径进行比较即可得出⊙M与直线AB的位置关系;
(2)根据(1)得出MD>MP,OM>MP,从而△OMP是等腰三角形可分两种情况讨论,①OP=MP,②OM=OP,分别运用相似三角形的性质求解OA即可;
(3)先表示出NF、BF,从而可得出OF的表达式,由⊙N和⊙O外切,可得出ON=x+y,在Rt△NFB中利用勾股定理,可得出y与x的关系式,也可得出自变量的定义域
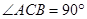 ,
,∵
 ,
,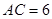
∴
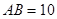 ,
, (1分)
(1分)过点
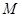 作
作 ,垂足为
,垂足为 . (1分)
. (1分)在
 中,
中,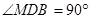 ,∴
,∴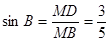 ,
, ∵
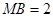 ,
,∴
 >
>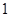 (1分)
(1分)∴⊙
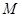 与直线
与直线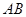 相离. (1分)
相离. (1分)解:(2)分三种情况:
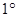 ∵
∵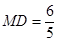 >
>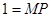 ,
,∴
 >
>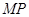 ; (1分)
; (1分)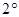 当
当 时,易得
时,易得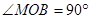 ,
,∴
 ,
,∴
 ,
,∴
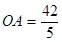 ; (2分)
; (2分)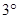 当
当 时,过点
时,过点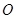 作
作 ,垂足为
,垂足为 .
.∴
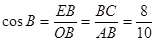 ,
,∴
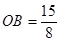 ,
,∴
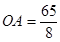 . (2分)
. (2分) 综合
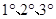 ,当
,当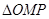 是等腰三角形时,
是等腰三角形时,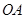 的长为
的长为 或
或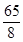 .
. 解:(3)联结
 ,过点
,过点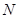 作
作 ,垂足为
,垂足为 .
.在
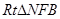 中,
中,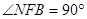 ,
,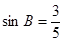 ,
,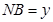 ;
;∴
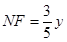 ,
, ;
;∴
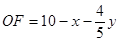 , (1分)
, (1分)∵⊙
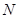 和⊙
和⊙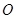 外切,
外切,∴
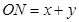 ; (1分)
; (1分)在
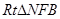 中,
中,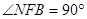 ,
,∴
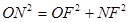 ;
;即
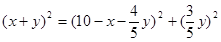 ;
;∴
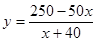 ; (2分)
; (2分)定义域为:
 <
<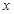 <
< .
.(1)过点M作MD⊥AB,垂足为D,根据MB=2,结合sin∠B的值,可得出MD的长,与圆M的半径进行比较即可得出⊙M与直线AB的位置关系;
(2)根据(1)得出MD>MP,OM>MP,从而△OMP是等腰三角形可分两种情况讨论,①OP=MP,②OM=OP,分别运用相似三角形的性质求解OA即可;
(3)先表示出NF、BF,从而可得出OF的表达式,由⊙N和⊙O外切,可得出ON=x+y,在Rt△NFB中利用勾股定理,可得出y与x的关系式,也可得出自变量的定义域

练习册系列答案
相关题目
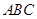 中,
中,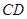 ⊥
⊥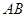 ,
,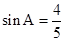 ,
,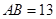 ,
,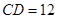 ,求
,求 的长和
的长和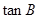 的值.
的值.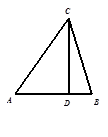
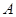 北偏西
北偏西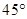 并距该岛
并距该岛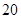 海里的
海里的 处待命.位于该岛正西方向
处待命.位于该岛正西方向 处的某渔船遭到袭扰,船长发现在其北偏东
处的某渔船遭到袭扰,船长发现在其北偏东 的方向有我海监84、75船编队(如图所示),便发出紧急求救信号.我海监84、75船编队接到信号后,立即沿
的方向有我海监84、75船编队(如图所示),便发出紧急求救信号.我海监84、75船编队接到信号后,立即沿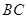 航线以每小时60海里的速度前去实施现场保护.问我海监84、75船编队需多少分钟可以到达该渔船所在的位置
航线以每小时60海里的速度前去实施现场保护.问我海监84、75船编队需多少分钟可以到达该渔船所在的位置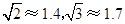 )
)
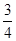 ;
;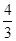 ;
;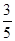 ;
;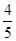 .
.

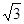 +1)m
+1)m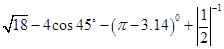 .
.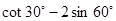
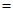 .
.