题目内容
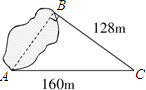 如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160m,BC长128m.问从点A到点B的距离有多远?
如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160m,BC长128m.问从点A到点B的距离有多远?
解:由题意得,∠ABC=90°,AC=160m,BC=128m,
在Rt△ABC中,AB= =96m.
=96m.
答:点A到点B的距离为96m.
分析:在Rt△ABC中,利用勾股定理求出AB即可得出答案.
点评:本题考查了勾股定理的应用,属于基础题,解答本题的关键是熟练掌握勾股定理的形式.
在Rt△ABC中,AB=
 =96m.
=96m.答:点A到点B的距离为96m.
分析:在Rt△ABC中,利用勾股定理求出AB即可得出答案.
点评:本题考查了勾股定理的应用,属于基础题,解答本题的关键是熟练掌握勾股定理的形式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间距离为
如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间距离为 如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使△ABC恰好为直角三角形(∠ABC=90°).通过测量,得到AC长为170m,BC长为150m,则从点A穿过湖到点B的距离为
如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使△ABC恰好为直角三角形(∠ABC=90°).通过测量,得到AC长为170m,BC长为150m,则从点A穿过湖到点B的距离为 如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160m,BC长128m.问从点A到点B的距离有多远?
如图,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160m,BC长128m.问从点A到点B的距离有多远? °,∠ABC=
°,∠ABC= °,又量得BC=
°,又量得BC= ,则A、B两点间的距离为
,则A、B两点间的距离为  (结果保留根号)
(结果保留根号)
