题目内容
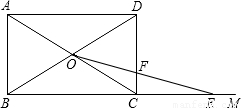
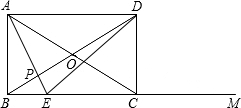
如图,C在射线BM上,在平行四边形ABCD中,AC=BD=10,tan∠CAD=| 3 | 4 |
(1)求CF的长;
(2)在没有“OC=CE”的条件下,连接DE、AE,AE与对角线BD相交于P点,若△ADE为等腰三角形,请求出DP的长.
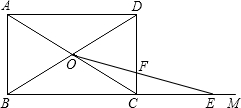
分析:(1)根据已知条件求得CD=6,讨论当E点在BC的延长线上时,CF的长,以及当E点在边BC上时,易证F在CD的延长线上,与题意不符,
(2)根据题意分情况进行解答,①交于BC的延长线上,②交于边BC,即可得出DP的长.
(2)根据题意分情况进行解答,①交于BC的延长线上,②交于边BC,即可得出DP的长.
解答:解:(1)∵ABCD为平行四边形且AC=BD,
∴ABCD为矩形,
∴∠ACD=90°
在RT△CAD中,tan∠CAD=
=
,
设CD=3k,AD=4k,
∴(3k)2+(4k)2=102,
解得k=2,
∴CD=3k=6,
(Ⅰ)当E点在BC的延长线上时,
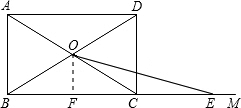
过O作OG⊥BC于G,
∴
=
=
,
∴OG=3
同理可得:
=
=
,即BG=GC=4,
又∵OC=CE=
AC=5,
∴
=
,
∴
=
解得CF=
,
(Ⅱ)当E点在边BC上时,易证F在CD的延长线上,与题意不符,舍去.
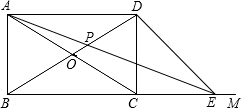
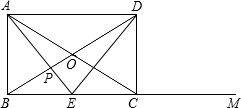
(2)若△ADE为等腰三角形,
(Ⅰ)AD=ED=8(交于BC的延长线上),
由勾股定理可得:CE=
=
=2
,
∵AD∥BE,
∴
=
=
=
,
设PD=4a,则BP=4a+
a,
∴BP+PD=BD=10=4a+
a+4a,
解得a=
,
∴PD=4a=
=
,
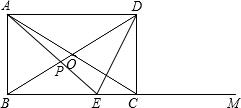
(Ⅱ)AD=ED=8(交于边BC),
同理可得:
=
=
=
,
∴BP+PD=BD=10=4a-
a+4a,
解得a=
,
∴PD=4a=
=
,
(Ⅲ)AE=ED,
易证:△AEB≌△DEC,
∴BE=EC=
BC=4,
∴同理可得:
=
,则
=
,
∴BP=
,PD=
,
(Ⅳ)AE=AD=8,
∴BE=
=2
∴同理可得:
=
=
,
∴PD=4a=
,
∴综上所述,若△ADE为等腰三角形,PD=
或
或
或
.
∴ABCD为矩形,
∴∠ACD=90°
在RT△CAD中,tan∠CAD=
| CD |
| AD |
| 3 |
| 4 |
设CD=3k,AD=4k,
∴(3k)2+(4k)2=102,
解得k=2,
∴CD=3k=6,
(Ⅰ)当E点在BC的延长线上时,
过O作OG⊥BC于G,
∴
| OG |
| CD |
| BO |
| BD |
| 1 |
| 2 |
∴OG=3
同理可得:
| BG |
| GC |
| BO |
| OD |
| 1 |
| 1 |
又∵OC=CE=
| 1 |
| 2 |
∴
| CF |
| OG |
| CE |
| EG |
∴
| CF |
| 3 |
| 5 |
| 5+4 |
解得CF=
| 5 |
| 3 |
(Ⅱ)当E点在边BC上时,易证F在CD的延长线上,与题意不符,舍去.
(2)若△ADE为等腰三角形,
(Ⅰ)AD=ED=8(交于BC的延长线上),
由勾股定理可得:CE=
| DE2-DC2 |
| 82-62 |
| 7 |
∵AD∥BE,
∴
| BE |
| AD |
| BP |
| PD |
8+2
| ||
| 8 |
4+
| ||
| 4 |
设PD=4a,则BP=4a+
| 7 |
∴BP+PD=BD=10=4a+
| 7 |
解得a=
10(8-
| ||
| 57 |
∴PD=4a=
40(8-
| ||
| 57 |
320-40
| ||
| 57 |
(Ⅱ)AD=ED=8(交于边BC),
同理可得:
| BP |
| PD |
| BE |
| AD |
8-2
| ||
| 8 |
4-
| ||
| 4 |
∴BP+PD=BD=10=4a-
| 7 |
解得a=
10(8+
| ||
| 57 |
∴PD=4a=
40(8+
| ||
| 57 |
320+40
| ||
| 57 |
(Ⅲ)AE=ED,
易证:△AEB≌△DEC,
∴BE=EC=
| 1 |
| 2 |
∴同理可得:
| BP |
| BD |
| 1 |
| 3 |
| BP |
| 10 |
| 1 |
| 3 |
∴BP=
| 10 |
| 3 |
| 20 |
| 3 |
(Ⅳ)AE=AD=8,
∴BE=
| 82-62 |
| 7 |
∴同理可得:
| BE |
| AD |
| ||
| 4 |
| BP |
| PD |
|
∴PD=4a=
160-40
| ||
| 9 |
∴综上所述,若△ADE为等腰三角形,PD=
320-40
| ||
| 57 |
320+40
| ||
| 57 |
| 20 |
| 3 |
160-40
| ||
| 9 |





点评:本题主要考查了平行线分线断成比例,全等三角形的判定,勾股定理以及矩形的判定与性质,比较综合,难度适中.

练习册系列答案
相关题目
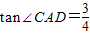 ,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.
,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.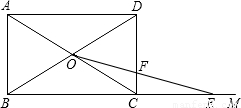
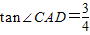 ,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.
,对角线AC与BD相交于O点.在射线BM上截取一点E,使OC=CE,连接OE,与边CD相交于点F.