��Ŀ����
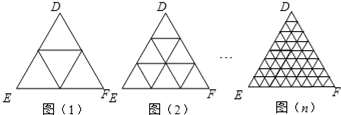
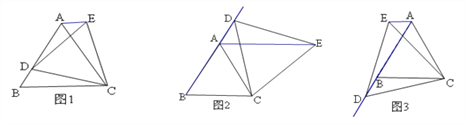
����Ŀ����1����ͼ1��D�ǵȱ���������ABC�ı�BA������һ�㣨D��A��B���غϣ�������DC����DCΪ����BC���Ϸ����ȱ���������DCE������AE����ABC���EAC������������ϵֱ��д������
��2����ͼ2��D�ǵȱ���������ABC��BA�ӳ�����һ�㣬����DC����DCΪ����BC���Ϸ����ȱ���������DCE������AE����֤����ABC=��EAC��
��3����ͼ3��D�ǵȱ���������ABC��AB�ӳ�����һ�㣬����DC����DCΪ����BC���Ϸ����ȱ���������DCE������AE��̽����ABC���EAC��������ϵ��ֱ��д������
���𰸡���1����ABC=��EAC����2��֤������������3����ABC +��EAC=180�����EAC=2��ABC
�������������������1�����ݵȱ������ε����ʵõ�CA=CB��CD=CE����ACB=��DCE=60��������SAS��֤����BCD�ա�ACE���̶��ó����ۣ���2��ͬ��1���ķ����жϳ���BCD�ա�ACE���ɣ���3��ͬ��1���ķ����жϳ���BCD�ա�ACE����.
���������
��1����ABC=��EAC��
����ABC����CDE�ǵȱ������Σ�
��CB=CA��CD=CE����ACB=��DCE=60����
���BCD=��ACE��
������BCD����ACE���� 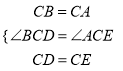
����BCD����ACE(SAS)��
���ABC=��EAC��
�ʴ�Ϊ����ABC=��EAC��
��2��֤��������ABC����DCE��Ϊ�ȱ�������
��CB=CA��CD=CE����ACB=��DCE =60����
���ACB+��DCA=��DCE+��DCA��
����DCB=��ECA��
����DCB����ECA����
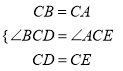
�� ��DCB�ա�EAC��
�� ��ABC=��EAC��
��3�� ��ABC +��EAC=180���� ��EAC=2��ABC
�ۡ���ABC����CDE�ǵȱ������Σ�
���ACB=��DCE=��ABC=60����
���ACE=��BCD��
����BCD����ACE����  ��
��
����BCD����ACE(SAS)��
���DBC=��EAC��
�ߡ�ABC+��DBC=180����
���ABC+��EAC=180����
�ߡ�ABC=60����
���EAC=120��=2��ABC.
�ʴ�Ϊ����ABC+��EAC=180�����EAC=2��ABC.

 �ۺ��Բ�ϵ�д�
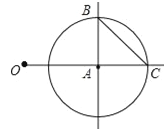
�ۺ��Բ�ϵ�д�����Ŀ�����������ļ�ֵ��֪ʶ�����ɼ����ͳ�����±����ɼ���91��100�ֵ�Ϊ��ʤ�ߣ�����ʤ�ߵ�Ƶ���ǣ�������
�ֶ������֣� | 61��70 | 71��80 | 81��90 | 91��100 |
�������ˣ� | 1 | 19 | 22 | 18 |
A. 35%B. 30%C. 20%D. 10%