题目内容
已知点(5-k2,2k+3)在第四象限内,且在其角平分线上,则k=________.
-2
分析:根据点的坐标,列出关于k的一元二次方程,然后利用配方法解方程即可.
解答:∵点(5-k2,2k+3)在第四象限内,
∴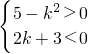 ,
,
解得- <x<-
<x<- ;
;
又∵点(5-k2,2k+3)在第四象限的角平分线上,
∴5-k2=-2k-3,即k2-2k-8=0,
∴k1=4(不合题意,舍去),k2=-2.
故答案是:-2.
点评:本题主要考查了点的坐标与解一元二次方程--配方法.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
分析:根据点的坐标,列出关于k的一元二次方程,然后利用配方法解方程即可.
解答:∵点(5-k2,2k+3)在第四象限内,
∴
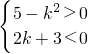 ,
,解得-
 <x<-
<x<- ;
;又∵点(5-k2,2k+3)在第四象限的角平分线上,
∴5-k2=-2k-3,即k2-2k-8=0,
∴k1=4(不合题意,舍去),k2=-2.
故答案是:-2.
点评:本题主要考查了点的坐标与解一元二次方程--配方法.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
 图象上,点C在函数
图象上,点C在函数