题目内容
已知直线y=| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 3 |
| 4k |
| 3 |
| 1 |
| 3 |
(1)求k的取值范围;
(2)若k为非负整数,△PAO是以OA为底的等腰三角形,点A的坐标为(2,0),点P在直线y=
| 1 |
| 2 |
| k |
| 2 |
分析:(1)先根据题意列出方程组,用k表示出x、y的值,再根据第四象限内点的坐标特点列出不等式组,求出k的取值范围即可;
(2)有(1)和k为非负整数则可求出k的值,再由已知条件可求出P点的坐标.
(2)有(1)和k为非负整数则可求出k的值,再由已知条件可求出P点的坐标.
解答:解:(1)解方程组
得:
∴直线y=
x+
-3和y=-
x+
+
的交点坐标为(k+4,k-1),
∵它们的交点在第四象限∴
解得:-4<k<1;
(2)∵k为非负整数,且-4<k<1,
∴k=0,则直线为:y=
x-3,
而O(0,0),A(2,0),
∴点P的横坐标为1,
代入y=
x-3中得:y=
×1-3=-
,
∴P(1,-
).
|
|
∴直线y=
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 3 |
| 4k |
| 3 |
| 1 |
| 3 |
∵它们的交点在第四象限∴
|
(2)∵k为非负整数,且-4<k<1,
∴k=0,则直线为:y=
| 1 |
| 2 |
而O(0,0),A(2,0),
∴点P的横坐标为1,
代入y=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴P(1,-
| 5 |
| 2 |
点评:本题考查了一次函数与一元一次不等式及解二元一次方程,属于基础题,关键是先求出交点确定k的坐标,再根据已知条件求解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 已知直线
已知直线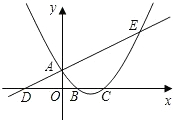 E两点,与x轴交于B、C两点,且B点坐标为(1,0).
E两点,与x轴交于B、C两点,且B点坐标为(1,0).
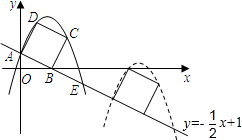 (2013•梧州模拟)如图,已知直线y=
(2013•梧州模拟)如图,已知直线y=