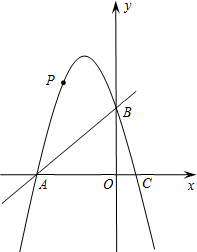题目内容
若点A在第二象限内，到x轴、y轴的距离为3和4，点B与点A关于原点对称，那么点B的坐标是（ ）
分析：根据一个点与y轴的距离等于横坐标的绝对值，结合各象限内点的坐标性质，得出A点坐标，再利用平面直角坐标系中任意一点P（x，y），关于原点的对称点的坐标是（-x，-y），即关于原点的对称点，横纵坐标都互为相反数得出即可．
解答：解：∵点A在第二象限内，到x轴、y轴的距离为3和4，
∴A点坐标为：（-4，3），
∵点B与点A关于原点对称，
∴点B的坐标是（4，-3）．
故选：D．
∴A点坐标为：（-4，3），
∵点B与点A关于原点对称，
∴点B的坐标是（4，-3）．
故选：D．
点评：此题主要考查了平面直角坐标系关于坐标轴成轴对称的两点的坐标之间的关系，是需要识记的内容．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知点A是反比例函数图象上一点，它到原点的距离为5，到x轴的距离为3，若点A在第二象限内，则这个反比例函数的表达式为（ ）
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
（2012•凉山州）如图，在平面直角坐标系中，直线y=x+4与x轴、y轴分别交于A、B两点，抛物线y=-x2+bx+c经过A、B两点，并与x轴交于另一点C（点C点A的右侧），点P是抛物线上一动点．