题目内容
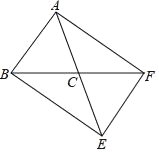
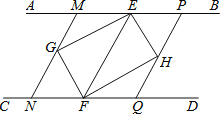
【题目】如图,AB∥CD,点 E、F 分别在 AB、CD 上,连接 EF.∠AEF、∠CF的平分线交于点 G,∠BEF、∠DFE 的平分线交于点 H.求证:四边形 EGFH 是矩形.
【答案】见解析
【解析】
利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠
EHF=90°,同法可得∠EGF=90°,再证明∠GEH=90°,进而求出四边形 EGFH 是矩形;
证明:∵EH 平分∠BEF,
∴![]()
∵FH 平分∠DFE,
∴![]()
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴![]()
∵∠FEH+∠EFH+∠EHF=180°,
∴∠EHF=180°﹣(∠FEH+∠EFH)=180°﹣90°=90°,
同理可得:∠EGF=90°,
∵EG 平分∠AEF,
∴![]()
∵EH 平分∠BEF,
∴![]()
∵点 A、E、B 在同一条直线上,
∴∠AEB=180°,
即∠AEF+∠BEF=180°,
![]() 即∠GEH=90°
即∠GEH=90°
∴四边形 EGFH 是矩形.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目