题目内容
已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=| 1 | 3 |
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
分析:(1)将A、B的横坐标代入抛物线的解析式中,即可求得A、B的坐标,然后将它们代入直线的解析式中,即可求得待定系数的值.
(2)根据抛物线的解析式不难得出其顶点实际是原点O,由于三角形OAB的面积无法直接求出,可将其化为其他图形面积的和差来求.设直线AB与x轴的交点为D,那么可用三角形ADO的面积减去三角形OBD的面积来求出三角形OAB的面积.可先根据直线AB的解析式求出D点坐标,然后根据上面分析的三角形ABO的面积计算方法进行求解即可.
(2)根据抛物线的解析式不难得出其顶点实际是原点O,由于三角形OAB的面积无法直接求出,可将其化为其他图形面积的和差来求.设直线AB与x轴的交点为D,那么可用三角形ADO的面积减去三角形OBD的面积来求出三角形OAB的面积.可先根据直线AB的解析式求出D点坐标,然后根据上面分析的三角形ABO的面积计算方法进行求解即可.
解答:解:(1)设A点坐标为(3,m);B点坐标为(-1,n).
∵A、B两点在y=
x2的图象上,
∴m=
×9=3,
n=
×1=
.
∴A(3,3),B(-1,
).
∵A、B两点又在y=ax+b的图象上,
∴
.
解得
.
∴一次函数的表达式是y=
x+1.
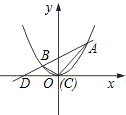
(2)如下图,
设直线AB与x轴的交点为D,则D点坐标为(-
,0).
∴|DC|=
.
S△ABC=S△ADC-S△BDC
=
×
×3-
×
×
=
-
=2.
∵A、B两点在y=
| 1 |
| 3 |
∴m=
| 1 |
| 3 |
n=
| 1 |
| 3 |
| 1 |
| 3 |
∴A(3,3),B(-1,
| 1 |
| 3 |
∵A、B两点又在y=ax+b的图象上,
∴
|
解得
|
∴一次函数的表达式是y=
| 2 |
| 3 |

(2)如下图,
设直线AB与x轴的交点为D,则D点坐标为(-
| 3 |
| 2 |
∴|DC|=
| 3 |
| 2 |
S△ABC=S△ADC-S△BDC
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
=
| 9 |
| 4 |
| 1 |
| 4 |
点评:本题考查了一次函数解析式的确定、图形面积的求法等知识,不规则图形的面积通常转化为规则图形的面积的和差.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目