题目内容
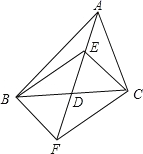
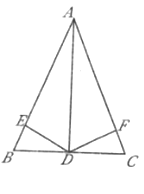
【题目】如图,![]() 是等腰
是等腰![]() 的顶角的平分线,
的顶角的平分线,![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上,且
上,且![]() 平分
平分![]() ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先根据ASA证明△AED≌△AFD,得到AE=AF,DE=DF,∠AED=∠AFD,进而得到BE=FC,∠BED=∠CFD,从而证明△BED≌△CFD,再判断各选项.
∵AD是等腰△ABC的顶角的平分线,AD平分∠EDF,
∴∠DAE=∠DAF,∠EDA=∠FDA,
在△ADE和△ADF中
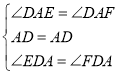 ,
,
∴△ADE≌△ADF(ASA).
∴AE=AF,DE=DF,∠AED=∠AFD,
∴∠BED=∠CFD,
∵△ABC是等腰三角形,
∴AB=AC,
又∵AE=AF,
∴BE=CF,(故A选项正确)
在△BED和△CFD中,
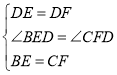 ,
,
∴△BED≌△CFD(SAS),
∴![]() ,
,![]() .(故B、C正确).
.(故B、C正确).
故选:D.

练习册系列答案
相关题目