Question

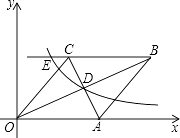
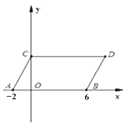
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－2，0)，(6，0)，现同时将点A，B分别向上平移4个单位，再向右平移2个单位，分别得到点A，B的对应点C、D，连接AC、BD．

(1)求点C，D的坐标及四边形ABDC的面积S四边形ABDC

(2)在y轴上是否存在一点P，连接PA、PB，使S△PAB=S四边形ABDC，若存在这样一点，求出点P的坐标，若不存在，试说明理由．

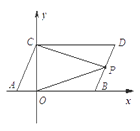
(3)点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时(不与B，D重合)给出下列结论：①的值不变;②的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．

Answer 1

【答案】（1）C（0，4），D（8，4），S四边形ABDC=32；（2）存在，P（0，8）或（0，-8）；（3）结论①正确， =1．

【解析】

（1）根据平移规律，直接得出点C，D的坐标，根据四边形ABDC的面积=AB×OC求解；
（2）存在．设点P到AB的距离为h，则S△PAB=×AB×h，根据S△PAB=S四边形ABDC，列方程求h的值，确定P点坐标；
（3）结论①正确，过P点作PE∥AB交OC与E点，根据平行线的性质得∠DCP+∠BOP=∠CPE+∠OPE=∠CPO，故比值为1．

解：（1）依题意，得C（0，4），D（8，4），
∴S四边形ABDC=AB×OC=8×4=32；

（2）存在．
设点P到AB的距离为h，
S△PAB=×AB×h=4h，
由S△PAB=S四边形ABDC，得4h=32，解得h=8，
∴P（0，8）或（0，-8）；
（3）结论①正确，

过P点作PE∥AB交OC与E点，
∵AB∥PE∥CD，
∴∠DCP+∠BOP=∠CPE+∠OPE=∠CPO，
∴ =1．

故答案为：（1）C（0，4），D（8，4），S四边形ABDC=32；（2）存在，P（0，8）或（0，-8）；（3）结论①正确， =1．