题目内容
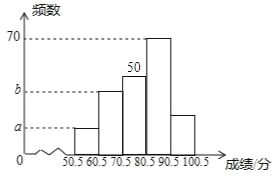
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:

(1)若A组的频数比B组小24,求频数分布直方图中的a、b的值;
(2)扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?
【答案】(1)16,40;(2)126,补图见解析;(3)940人.
【解析】
试题分析:(1)根据若A组的频数比B组小24,且已知两个组的百分比,据此即可求得总人数,然后根据百分比的意义求得a、b的值;
(2)利用360°乘以对应的比例即可求解;
(3)利用总人数乘以对应的百分比即可求解.
试题解析:(1)学生总数是24÷(20%-8%)=200(人),
则a=200×8%=16,b=200×20%=40;
(2)n=360×![]() =126°.
=126°.
C组的人数是:200×25%=50.
 ;
;
(3)样本D、E两组的百分数的和为1-25%-20%-8%=47%,
∴2000×47%=940(名)
答估计成绩优秀的学生有940名.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目