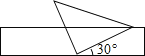
题目内容
【题目】如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )

A.2﹣![]() B.2+
B.2+![]() C.
C.![]() ﹣2 D.
﹣2 D.![]() +1
+1
【答案】B
【解析】
试题分析:根据扥国药三角形的性质得∠A=∠ADB,再利用三角形外角性质可计算出∠A=15°,则∠ADC=75°,设CD=a,在Rt△BCD中,根据含30度的直角三角形三边的关系得到BD=2a,BC=![]() a,则AC=(2+
a,则AC=(2+![]() )a,然后在Rt△ACD中利用正切的定义求解.
)a,然后在Rt△ACD中利用正切的定义求解.
解:∵AB=BD,
∴∠A=∠ADB,
∵∠DBC=∠A+∠ADB=30°,
∴∠A=15°,
∴∠ADC=75°,
设CD=a,
在Rt△BCD中,
∵∠DBC=30°,
∴BD=2a,BC=![]() a,
a,
∴AC=AB+BC=BD+BC=2a+![]() a=(2+
a=(2+![]() )a,
)a,
在Rt△ACD中,tan∠ADC=tan75°=![]() =
=![]() =2+
=2+![]() .
.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目