题目内容
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.

(1)求证:DE与⊙O相切;
(2)若⊙O的半径为![]() ,DE=3,求AE的长.
,DE=3,求AE的长.
答案:
解析:
解析:
|
分析:(1)欲证“DE与⊙O相切”,因为点E在⊙O上,如果结论成立,则点E肯定是切点,所以只需连接OE,证明OE⊥ED即可;(2)利用△ABE∽△ACB可求AE的长. 解:(1)连接OE、BE, 因为AB是直径, 所以BE⊥AC. 因为D是BC的中点, 所以DE=DB. 所以∠DBE=∠DEB. 又OE=OB,∠OBE=∠OEB, 所以∠DBE+∠OBE=∠DEB+∠OEB, 即∠ABD=∠OED. 又∠ABC=90°,所以∠OED=90°. 所以DE是⊙O的切线. (2)因为DE=3,所以BC=2DE=6. 所以AC= 又△ABE∽△ACB,所以 所以AE= 点评:证明切线时,条件中给出了直线与圆的公共点,但未给出过这点的半径,则连接公共点和圆心,然后根据“经过半径的一端且垂直于这条半径的直线是圆的切线”这个定理进行证明.口诀是“连半径,证垂直.切线判断很简单,认真审题是关键”. |

练习册系列答案
相关题目
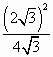 =
=
 .
. 如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( ) 如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.
如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.