Question

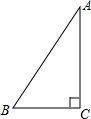
如图，△ABC是直角三角形，∠BAC=90°，AD、AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm．
（1）求AD的长；
（2）求△AEC的面积．

Answer 1

分析：（1）利用“面积法”来求线段AD的长度；
（2）△AEC与△ABE的等底同高的两个三角形，它们的面积相等．

解答：解：∵∠BAC=90°，AD是边BC上的高，
∴

1

2

AB•AC=

1

2

BC•AD，
∴AD=

AB•AC

BC

=

6×8

10

=4.8（cm），即AD的长度为4.8cm；

（2）如图，∵△ABC是直角三角形，∠BAC=90°，AB=6cm，AC=8cm，
∴S_△ABC=

1

2

AB•AC=

1

2

×6×8=24（cm²）．
又∵AE是边BC的中线，
∴BE=EC，
∴

1

2

BE•AD=

1

2

EC•AD，即S_△ABE=S_△AEC，
∴S_△AEC=

1

2

S_△ABC=12（cm²）．
∴△AEC的面积是12cm²．

点评：本题考查了三角形的面积．
（1）三角形的面积等于底边长与高线乘积的一半，即S_△=

1

2

×底×高．
（2）三角形的中线将三角形分成面积相等的两部分．