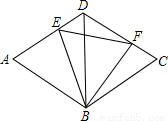
题目内容
如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.
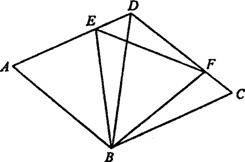
(1)求证:△BDF≌△BCF;
(2)判断△BEF的形状,并说明理由.同时指出△BCF是由△BDE经过如何变换得到?
答案:
解析:
解析:
|
证明:(1)∵菱形ABCD的边长为2,BD=2. ∴BD=BC且∠BDE=∠8CF=60°. ∵AE+CF=2. 又∵AE+DE=AD=2 ∴DE=CF ∴△BDE≌△BCF 4分 (2)△BEF是等边三角形 6分 理由如下:由(1)得:△BDE≌△BCF ∴BE=BF,∠CBF=∠DBE. ∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60° ∴△BEF是等边三角形. 7分 △BCF是由△BDE绕点B顺时针旋转60°得到. 8分 |

练习册系列答案
相关题目
 (2011•泰宁县质检)如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.
(2011•泰宁县质检)如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.
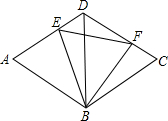 如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.
如图菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.