题目内容
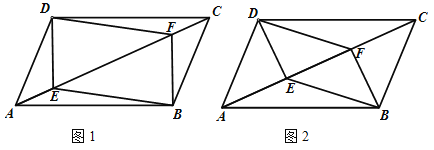
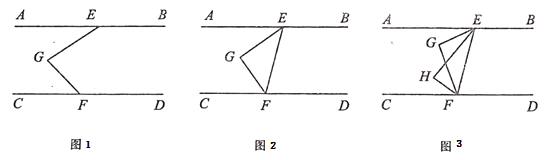
【题目】(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数。证明你的猜想
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
【答案】（1）见解析；（2）∠G＝90°；证明见解析；（3）∠H＝85°.
【解析】
（1）过点G作GH∥AB，根据两直线平行内错角相等可证得结论；
（2）由（1）得∠EGF＝∠AEG＋∠CFG，根据EG、FG分别平分∠AEF和∠CFE，得到∠AEF＝2∠AEG，∠CFE＝2∠CFG，由于AB∥CD得到∠AEF＋∠CFE＝180°，于是得到2∠AEG＋2∠CFG＝180°，即可得到结论；
（3）由（1）得∠G＝∠AEG＋∠CFG，∠H＝∠AEH＋∠CFH，根据EG平分∠AEH，EH平分∠GEF，FH平分∠CFG，FG平分∠HFE，分别得到∠AEG＝∠GEH＝∠HEF＝
∠AEF，∠CFH＝∠HFG＝∠EFG＝∠CFE，结合∠AEF＋∠CFE＝180°，于是可求出∠CFE＝105°，∠AEF＝75°，代入∠H＝
∠AEF＋∠CFE，计算即可得到结论．
解：（1）如图1，
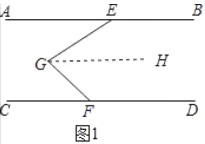
过点G作GH∥AB，
∴∠EGH＝∠AEG．
∵AB∥CD，
∴GH∥CD．
∴∠FGH＝∠CFG．
∴∠EGH＋∠FGH＝∠AEG＋∠CFG．
即∠EGF＝∠AEG＋∠CFG；
（2）猜想：∠G＝90°；
证明：如图2，
由（1）中的结论得：∠EGF＝∠AEG＋∠CFG，
∵EG、FG分别平分∠AEF和∠CFE，
∴∠AEF＝2∠AEG，∠CFE＝2∠CFG，
∵AB∥CD，
∴∠AEF＋∠CFE＝180°，
∴2∠AEG＋2∠CFG＝180°，
∴∠AEG＋∠CFG＝90°，
∴∠G＝90°；
（3）解：如图3，
∵EG平分∠AEH，EH平分∠GEF，FH平分∠CFG，FG平分∠HFE，
∴∠AEG＝∠GEH＝∠HEF＝∠AEF，∠CFH＝∠HFG＝∠EFG＝∠CFE，
由（1）可知，∠G＝∠AEG＋∠CFG，∠H＝∠AEH＋∠CFH，
∴∠G＝∠AEF＋∠CFE＝95°，
∴（∠AEF＋∠CFE）＋∠CFE＝95°，
∵AB∥CD，
∴∠AEF＋∠CFE＝180°，
∴∠CFE＝105°，
∴∠AEF＝75°，
∴∠H＝∠AEF＋∠CFE＝×75°＋×105°＝85°．
