题目内容
已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为切点.(1)当OP为何值时,∠APB=90°?
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据sin50°=0.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,cos25°=0.9063,tan25°=0.4663)
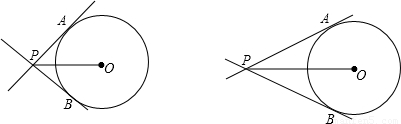
【答案】分析:(1)连接OA,OP平分∠PAB,若△PAB是等腰直角三角形,那么∠OPA=45°,利用∠APO的正弦值即可求出OP的长;
(2)连接OA,OP平分∠PAB,则∠APO=25°,利用∠APO的正切值即可求出AP的长.
解答: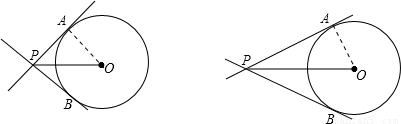 解:(1)连接OA,(1分)
解:(1)连接OA,(1分)
∵PA,PB是⊙O的切线,
∴∠PAO=90°,∠APO=∠BPO,
∵∠APB=90°
∴∠APO=45°
sin45°=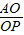 =
=
∴OP=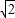 AO=8
AO=8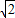 ;
;
(2)连接OA,
∵PA,PB是⊙O的切线
∴∠APO=∠BPO= ∠APB=25°,
∠APB=25°,
∵tan25°=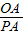 ,
,
∴PA=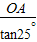 =
=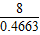 ≈17.2.
≈17.2.
点评:本题考查切线的性质和锐角的三角函数.
(2)连接OA,OP平分∠PAB,则∠APO=25°,利用∠APO的正切值即可求出AP的长.
解答:
 解:(1)连接OA,(1分)
解:(1)连接OA,(1分)∵PA,PB是⊙O的切线,
∴∠PAO=90°,∠APO=∠BPO,
∵∠APB=90°
∴∠APO=45°
sin45°=
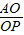 =
=
∴OP=
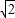 AO=8
AO=8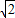 ;
;(2)连接OA,
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=
 ∠APB=25°,
∠APB=25°,∵tan25°=
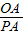 ,
,∴PA=
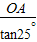 =
=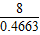 ≈17.2.
≈17.2.点评:本题考查切线的性质和锐角的三角函数.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
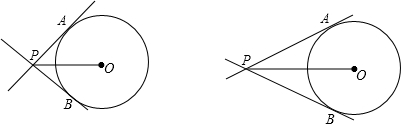
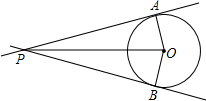 为A,B.
为A,B.