题目内容
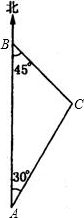某轮船沿正北方向航行，在A点处测得灯塔C在北偏东30°，航行20海里后到达B点．在B点处测得灯塔C在南偏东45°，求轮船此时距灯塔C的距离（结果保留根号）
分析：作CD⊥AB于D，构建两个直角三角形，利用两个已知角的正切值求出CD的长，进而就可以求得BC的长．
解答：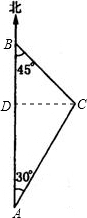
解：作CD⊥AB于D，设BD=x，则AD=20-x
在△BCD中，∠BCD=45°
∴CD=x
在直角△ACD中，tanA=
∴x=10
-10
在直角△BCD中，sin∠CBD=
∴
=
∴BC=10
-10
海里
答：轮船此时距灯塔C的距离10
-10
海里．
解：作CD⊥AB于D，设BD=x，则AD=20-x在△BCD中，∠BCD=45°
∴CD=x
在直角△ACD中，tanA=
| CD |
| AD |
∴x=10
| 3 |
在直角△BCD中，sin∠CBD=
| CD |
| BC |
∴
| ||
| 2 |
10
| ||
| BC |
∴BC=10
| 6 |
| 2 |
答：轮船此时距灯塔C的距离10
| 6 |
| 2 |
点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
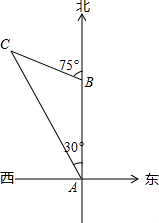如图，某轮船沿正北方向航行，在点A处测得灯塔C在北偏西30°处．轮船以每小时20海里的速度航行，2小时到达点B后，测得灯塔C在轮船北偏西75°处．当该轮船继续 航行到达灯塔C的正东方向时，求此时轮船与灯塔C之间的大致距离．（结果精确到0.1海里，参考数据：
）
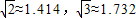