题目内容
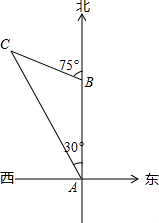 如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据:
如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据:| 2 |
| 3 |
分析:首先作BD⊥AC于点D,作CE⊥AB于点E,进而得出△CDB为等腰直角三角形,再利用CE=
AC求出即可.
| 1 |
| 2 |
解答: 解:作BD⊥AC于点D,作CE⊥AB于点E,
解:作BD⊥AC于点D,作CE⊥AB于点E,
AB=40海里,
BD=40sin30°=20,
AD=40cos30°=20
,
△CDB为等腰直角三角形,
CD=BD=20,
Rt△ACE中,∠CAE=30° AC=20+20
,
∴CE=
AC=10+10
≈27.3(海里),
答:此时轮船与灯塔C之间的距离约为27.3海里.
 解:作BD⊥AC于点D,作CE⊥AB于点E,
解:作BD⊥AC于点D,作CE⊥AB于点E,AB=40海里,
BD=40sin30°=20,
AD=40cos30°=20
| 3 |
△CDB为等腰直角三角形,
CD=BD=20,
Rt△ACE中,∠CAE=30° AC=20+20
| 3 |
∴CE=
| 1 |
| 2 |
| 3 |
答:此时轮船与灯塔C之间的距离约为27.3海里.
点评:此题主要考查了方向角问题的应用,根据已知得出△CDB为等腰直角三角形以及在直角三角形中求出AC的长是解题关键.

练习册系列答案
相关题目
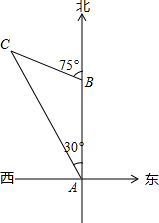
 如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据:
如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据: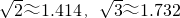 )
)
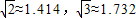 )
)