题目内容
(2005•宁德)如图,直线y=kx+8分别与x轴、y轴相交于A、B两点,O为坐标原点,A点的坐标为(4,0).(1)求k的值;
(2)若P为y轴(B点除外)上的一点,过P作PC⊥y轴交直线AB于C.设线段PC的长为l,点P的坐标为(0,m).
①如果点P在线段BO(B点除外)上移动,求l与m的函数关系式,并写出自变量m的取值范围;
②如果点P在射线BO(B、O两点除外)上移动,连接PA,则△APC的面积S也随之发生变化.请你在面积S的整个变化过程中,求当m为何值时,S=4.

【答案】分析:(1)A点的坐标满足解析式y=kx+8,就可以求出函数的解析式;
(2)根据PC⊥y轴,OA⊥y轴,得到PC∥OA,则△BPC∽△BOA,根据相似三角形的对应边的比相等,就可以求出.
解答: 解:(1)∵点A(4,0)在直线y=kx+8上,
解:(1)∵点A(4,0)在直线y=kx+8上,
∴0=k×4+8,
解得k=-2;
(2)①如图①,由(1)得直线AB的解析式为y=-2x+8,
由x=0,解得y=8,
∴B(0,8),
∴0≤m<8.
设c(x,y),由y=m=-2x+8,
解得x=4- m>0,
m>0,
∴PC=4- m,
m,
即所求l与m的函数关系式为l=4- m(0≤m<8);
m(0≤m<8);
②如图②,
当0<m<8时,s= PC•PO=
PC•PO= (4-
(4- m)•m
m)•m
=- m2+2m,
m2+2m,
由- m2+2m=4.解得m1=m2=4;
m2+2m=4.解得m1=m2=4;
如图③,当m<0时,同①可求得PC=4- m,又PO=-m,
m,又PO=-m,
∴S= PC•PO=
PC•PO= (4-
(4- m)•(-m)=
m)•(-m)= m2-2m,
m2-2m,
由 m2-2m=4,解得m1=4+4
m2-2m=4,解得m1=4+4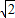 >0(舍去),
>0(舍去),
m2=4-4 ,
,
综上,当m=4或m=4-4 时,S=4.
时,S=4.
点评:本题主要考查了待定系数法求函数解析式,注意分情况讨论是解决本题的关键.
(2)根据PC⊥y轴,OA⊥y轴,得到PC∥OA,则△BPC∽△BOA,根据相似三角形的对应边的比相等,就可以求出.
解答:
 解:(1)∵点A(4,0)在直线y=kx+8上,
解:(1)∵点A(4,0)在直线y=kx+8上,∴0=k×4+8,
解得k=-2;
(2)①如图①,由(1)得直线AB的解析式为y=-2x+8,
由x=0,解得y=8,
∴B(0,8),
∴0≤m<8.
设c(x,y),由y=m=-2x+8,
解得x=4-
 m>0,
m>0,∴PC=4-
 m,
m,即所求l与m的函数关系式为l=4-
 m(0≤m<8);
m(0≤m<8);②如图②,
当0<m<8时,s=
 PC•PO=
PC•PO= (4-
(4- m)•m
m)•m=-
 m2+2m,
m2+2m,由-
 m2+2m=4.解得m1=m2=4;
m2+2m=4.解得m1=m2=4;如图③,当m<0时,同①可求得PC=4-
 m,又PO=-m,
m,又PO=-m,∴S=
 PC•PO=
PC•PO= (4-
(4- m)•(-m)=
m)•(-m)= m2-2m,
m2-2m,由
 m2-2m=4,解得m1=4+4
m2-2m=4,解得m1=4+4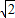 >0(舍去),
>0(舍去),m2=4-4
 ,
,综上,当m=4或m=4-4
 时,S=4.
时,S=4.点评:本题主要考查了待定系数法求函数解析式,注意分情况讨论是解决本题的关键.

练习册系列答案
相关题目



