题目内容
 24、如图,已知AB⊥BC,CD⊥BC,∠AMB=75°,∠DMC=45°,AM=MD.求证:AB=BC.
24、如图,已知AB⊥BC,CD⊥BC,∠AMB=75°,∠DMC=45°,AM=MD.求证:AB=BC.分析:先过A作AE⊥CD,交CD的延长线于点E,由于AB⊥BC,CD⊥BC,AE⊥CD,易证四边形ABCE是长方形,而∠AMB=75°,∠DMC=45°,可求∠AMD=60°,∠CDM=45°,而AM=DM,那么△AMD是等边三角形,于是∠ADM=∠MAD=60°,AM=AD,∠ADE=75°,利用AAS可证△ADE≌△AMB,可得AB=AE,易证四边形ABCE是正方形,从而有AB=BC.
解答: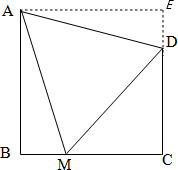 证明:如右图所示,过A作AE⊥CD,交CD的延长线于点E,
证明:如右图所示,过A作AE⊥CD,交CD的延长线于点E,
∵AB⊥BC,CD⊥BC,AE⊥CD,
∴∠B=∠C=∠E=90°,
∴四边形ABCE是长方形,
∵∠AMB=75°,∠DMC=45°,
∴∠AMD=60°,∠CDM=45°,
又∵AM=MD,
∴△AMD是等边三角形,
∴∠ADM=∠MAD=60°,AM=AD,∠ADE=75°,
∴∠CDM=45°,
∴∠CMD=45°,
∴CD=CM,
∴DE=BM,
∴△ADE≌△AMB,
∴AB=AE,
∴四边形ABCE是正方形,
∴AB=BC.
 证明:如右图所示,过A作AE⊥CD,交CD的延长线于点E,
证明:如右图所示,过A作AE⊥CD,交CD的延长线于点E,∵AB⊥BC,CD⊥BC,AE⊥CD,
∴∠B=∠C=∠E=90°,
∴四边形ABCE是长方形,
∵∠AMB=75°,∠DMC=45°,
∴∠AMD=60°,∠CDM=45°,
又∵AM=MD,
∴△AMD是等边三角形,
∴∠ADM=∠MAD=60°,AM=AD,∠ADE=75°,
∴∠CDM=45°,
∴∠CMD=45°,
∴CD=CM,
∴DE=BM,
∴△ADE≌△AMB,
∴AB=AE,
∴四边形ABCE是正方形,
∴AB=BC.
点评:本题考查了全等三角形的判定和性质、正方形的判定和性质、长方形的判定、等边三角形的判定和性质.解题的关键是作辅助线,构造正方形.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
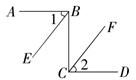 22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.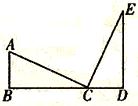 22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.
22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.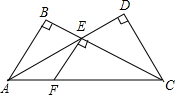 如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有:
如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有: 如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为
如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为 如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.
如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.