题目内容
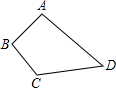 如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为
如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为分析:连接AB,根据勾股定理可求出AC的长,根据△ACD的三边关系可求出△ACD为直角三角形,再利用两直角三角形面积的和即可求解.
解答: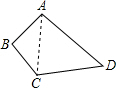 解:连接AC,
解:连接AC,
∵AB⊥BC于B,BC=4,AB=3,
∴AC=
=
=5;
在△ACD中,∵CD=12,AD=13,AC=5,52+122=132,即AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC,
=
AB•BC+
CD•AC,
=
×3×4+
×12×5,
=6+30,
=36.
故答案为:36.
 解:连接AC,
解:连接AC,∵AB⊥BC于B,BC=4,AB=3,
∴AC=
| AB2+BC2 |
| 42+32 |
在△ACD中,∵CD=12,AD=13,AC=5,52+122=132,即AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=6+30,
=36.
故答案为:36.
点评:本题考查勾股定理的逆定理的应用.解答此题的关键是作出辅助线,构造出直角三角形,求出AC的长,再判断出△ACD为直角三角形,再利用三角形的面积公式即可解答.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由. 22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.
22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由. 如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有:
如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有: 如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.
如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.