题目内容
如图,圆(直径为
)的切点分别为A,B,C,那么图中的距离x=______.(用最简分数表示).

| 3 |
| 8 |

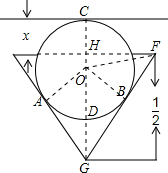
连接CO、OG、OF、OB,CO交EF于点H.
∵⊙O的直径是
∴OC=OB=
,GH=
,HC=x
∴OH=
-x
∵△GEF是等边三角形
∴∠OGF=30°
∴GF=2HF
在Rt△GHF中,由勾股定理,得
HF=
,GF=
,
在Rt△HOF中,由勾股定理,得
OF2=(
)2+(
-x)2
在Rt△OBG中,由勾股定理,得
GB=
,BF=
-
在Rt△OBF中,由勾股定理,得
(
)2+(
-x)2-(
)2=(
-
)2,
解得:x1=
(不符合题意,舍去),x2=
.
故答案为:
.
∵⊙O的直径是
| 3 |
| 8 |
∴OC=OB=
| 3 |
| 16 |
| 1 |
| 2 |
∴OH=
| 3 |
| 16 |
∵△GEF是等边三角形
∴∠OGF=30°
∴GF=2HF
在Rt△GHF中,由勾股定理,得
HF=
| ||
| 6 |
| ||
| 3 |
在Rt△HOF中,由勾股定理,得
OF2=(
| ||
| 6 |
| 3 |
| 16 |
在Rt△OBG中,由勾股定理,得
GB=
3
| ||
| 16 |
| ||
| 3 |
3
| ||
| 16 |
在Rt△OBF中,由勾股定理,得
(
| ||
| 6 |
| 3 |
| 16 |
| 3 |
| 16 |
| ||
| 3 |
3
| ||
| 16 |
解得:x1=
| 5 |
| 8 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |


练习册系列答案
相关题目
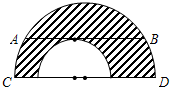





 轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.
轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.