题目内容
【题目】（满分8分） 已知：如图，在正方形ABCD中，F是AB上一点，延长CB到E，使BE=BF，连接CF并延长交AE于G．
（1）求证：△ABE≌△CBF；
（2）将△ABE绕点A逆时针旋转90°得到△ADH，请判断四边形AFCH是什么特殊四边形，并说明理由．
【答案】(1) 证明见解析;(2) 证明见解析.
【解析】试题分析：（1）由于四边形ABCD是正方形，所以AB=CB=DC，因为AB∥CD，∠CBA=∠ABE，从而得证．
（2）根据旋转的性质可知△ABE≌△ADH，从而可证AF=CH，然后利用AB∥CD即可知四边形AFCH是平行四边形.
试题解析：
（1）证明： 
∴
，AB//CD
∴
∴
在△ABE和△CBF中
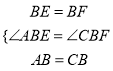
∴△ABE≌△CBF（SAS）
（2）答：四边形AFCH是平行四边形
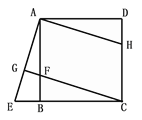
理由：∵△ABE绕点A逆时针旋转90°得到△ADH
∴△ABE≌△ADH
∴BE=DH
又∵BE=BF（已知）
∴BF=DH(等量代换)
又∵AB=CD（由（1）已证）
∴AB-BF=CD-DH
即AF=CH
又∵AB//CD 即AF//CH
∴四边形AFCH是平行四边形
练习册系列答案
文敬图书课时先锋系列答案
相关题目
