题目内容
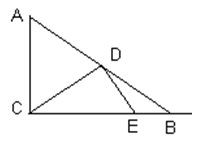
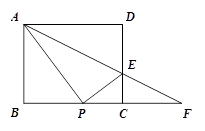
如图,已知在Rt△ABC中,∠ACB=90°,AB=10,tanA=4/3,点D是斜边AB上的动点,连接CD,作DE⊥CD,交射线CB于点E,设AD=x。(1)当点D是边AB的中点时,求线段DE的长;(2)当△BED是等腰三角形时,求x的值;(3)如果y=DE/DB。求y关于x的函数解析式,并写出它的定义域。

(1)DE=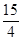 ;(2)(i)x=
;(2)(i)x=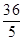 ;(ii)AD=2;(3)y=
;(ii)AD=2;(3)y=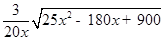 (0<x<10).
(0<x<10).
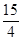 ;(2)(i)x=
;(2)(i)x=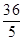 ;(ii)AD=2;(3)y=
;(ii)AD=2;(3)y=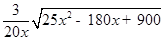 (0<x<10).
(0<x<10).试题分析:(1)在直角三角形ABC中,由AB与tanA的值,利用锐角三角函数定义及勾股定理求出BC与AC的长,由D为斜边上的中点,利用直角三角形斜边上的中线等于斜边的一半得到CD=AD=BD=5,可得出∠DCB=∠DBC,再由一对直角相等,利用两对对应角相等的三角形相似得到△EDC与△ACB相似,由相似得比例,即可求出DE的长;
(2)分两种情况考虑:
(i)当E在BC边上时,由△BDE为等腰三角形且∠BED为钝角,得到DE=BE,利用等边对等角得到∠EBD=∠EDB,利用等角的余角相等得到∠CDA=∠A,利用等角对等边得到CD=AC,作CH垂直于AB,利用三线合一得到AD=2AH,由cosA的值求出AH的长,进而求出AD的长,即为x的值;
(ii)当E为BC延长线上时,与∠DBE为钝角得到DB=BE,同理求出x的值;
(3)作DM垂直于BC,得到DM与AC平行,由平行得比例,表示出DM与BM,进而表示出CD与CM,由三角形DEM与三角形CDM相似得比例,表示出DE,由BD=AB-AD=10-x,将DE与DB代入表示出y,化简得到结果,并求出x的范围即可.
试题解析:
(1)在△ABC中,∵∠ACB=90°,AB=10,tanA="4" 3 ,
∴BC=8,AC=6,
∵点D为斜边AB的中点,∴CD=AD=BD=5,
∴∠DCB=∠DBC,
∵∠EDC=∠ACB=90°,
∴△EDC∽△ACB,
∴DE:CD="AC:BC" ,即DE:5="6:8" ,
则DE=
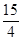 ;
;(2)分两种情况情况:
(i)当E在BC边长时,
∵△BED为等腰三角形,∠BED为钝角,
∴EB=ED,
∴∠EBD=∠EDB,
∵∠EDC=∠ACB=90°,
∴∠CDA=∠A,
∴CD=AC,
作CH⊥AB,垂足为H,那么AD=2AH,
∴AH:AC="3:5" ,即AH=
 ,
,∴AD=
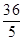 ,即x=
,即x=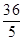 ;
;(ii)当E在CB延长线上时,
∵△BED为等腰三角形,∠DBE为钝角,
∴BD=DE,
∴∠BED=∠BDE,
∵∠EDC=90°,
∴∠BED+∠BCD=∠BDE+∠BDC=90°,
∴∠BCD=∠BDC,
∴BD=BC=8,
∴AD=x=AB-BD=10-8=2;
(3)作DM⊥BC,垂足为M,
∵DM∥AC,
∴DM:AC="BM:BC=BD:BA" ,
∴DM=
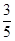 (10-x),BM=
(10-x),BM=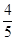 (10-x),
(10-x),∴CM=8-
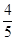 (10-x)=
(10-x)=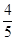 x,CD= x2?
x,CD= x2?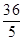 x+36 ,
x+36 ,∵△DEM∽△CDM,
∴DE:DM="CD:CM" ,即DE=
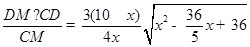 ,
,∴y=
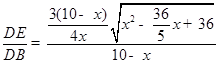 ,
,整理得:y=
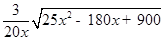 (0<x<10).
(0<x<10).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
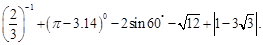 = .
= .
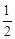 时,求a的值.
时,求a的值.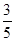 .
.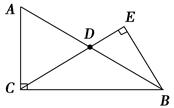
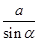 ;
;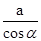
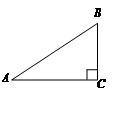
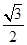
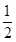
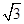
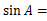 _ .
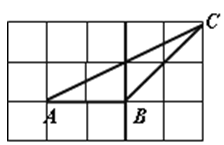
_ .
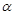 为一锐角,化简:
为一锐角,化简: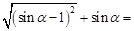 .
.