题目内容
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,A(-1,0).
(1)求这条抛物线的解析式;
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线的对称轴交于点E,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作QF⊥AE于F,QG⊥DB于G,请判断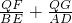 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;
(3)在(2)的条件下,若点H是线段EQ上一点,过点H作MN⊥EQ,MN分别与边AE、BE相交于M、N,(M与A、E不重合,N与E、B不重合),请判断 是否成立?若成立,请给出证明;若不成立,
是否成立?若成立,请给出证明;若不成立, 请说明理由.
请说明理由.
解:(1)设抛物线的解析式为y=a(x-1)2-4,
将A(-1,0)代入解析式得:0=a(-1-1)2-4,
∴a=1,
∵抛物线的解析式为y=(x-1)2-4,
即y=x2-2x-3;
(2)是定值, +
+ =1,
=1,
∵AB是直径,
∴∠AEB=90°,
∵QF⊥AE,
∴QF∥BE,
∴△AQF∽△ABE,
∴ =
=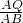 ,
,
同理: =
= ,
,
∴ +
+ =
=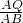 +
+ =
= =
= =1;
=1;
(3)∵直线EC为抛物线的对称轴,
∴EC垂直平分AB,
∴AE=EB,
∵∠AEB=90°,
∴△AEB为等腰直角三角形,
∴∠EAB=∠EBA=45°,
过点Q作QP⊥BE于P,如图
由已知及作法可知,四边形FQPE是矩形,
∴QP=FE且QP∥FE,
在△AQF和△QBP中,
∵∠EAB=∠BQP=45°,
∴QP=BP=FE且△AQF∽△QBP,
∴ =
= ,
,
∴ =
= =
= ①,
①,
在△QFE和△MEN中,
∵MN⊥EQ,
∴∠MNE+∠HEN=90°,
∵∠FEQ+∠HEN=90°,
∴∠MNE=∠FEQ,
又∵∠QFE=∠MEN=90°,
∴△EFQ∽△NEM,
∴ =
= ②,
②,
由①、②知: =
= .
.
分析:(1)可将抛物线的解析式设为顶点式,然后将A点坐标代入,即可求得抛物线的解析式;
(2)根据两对相似三角形:△AQF、△ABE和△BGQ、△BDA得出的对应成比例线段,即可求出所求的代数式是否为定值;
(3)易证得△EMN∽△FQE,得 ①,下面证
①,下面证 ,需通过构建相似三角形求解;
,需通过构建相似三角形求解;
过Q作QP⊥BE于P,则四边形FQPE是矩形,FE=QP②;已知E在AB的垂直平分线上,可得:△AEB是等腰Rt△,进一步可知△AFQ、△QEB也是等腰Rt△;易证得△FAQ∽△PQB,得 ③,联立①②③即可证得所求的结论.
③,联立①②③即可证得所求的结论.
点评:此题考查了二次函数解析式的确定、相似三角形的判定和性质、二次函数的性质、等腰直角三角形的判定和性质等知识;(3)题中,能够正确的根据已知和所求条件构建出相似三角形是解题的关键.
将A(-1,0)代入解析式得:0=a(-1-1)2-4,

∴a=1,
∵抛物线的解析式为y=(x-1)2-4,
即y=x2-2x-3;
(2)是定值,
 +
+ =1,
=1,∵AB是直径,
∴∠AEB=90°,
∵QF⊥AE,
∴QF∥BE,
∴△AQF∽△ABE,
∴
 =
=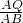 ,
,同理:
 =
= ,
,∴
 +
+ =
=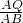 +
+ =
= =
= =1;
=1;(3)∵直线EC为抛物线的对称轴,
∴EC垂直平分AB,
∴AE=EB,
∵∠AEB=90°,
∴△AEB为等腰直角三角形,
∴∠EAB=∠EBA=45°,
过点Q作QP⊥BE于P,如图
由已知及作法可知,四边形FQPE是矩形,
∴QP=FE且QP∥FE,
在△AQF和△QBP中,
∵∠EAB=∠BQP=45°,
∴QP=BP=FE且△AQF∽△QBP,
∴
 =
= ,
,∴
 =
= =
= ①,
①,在△QFE和△MEN中,
∵MN⊥EQ,
∴∠MNE+∠HEN=90°,
∵∠FEQ+∠HEN=90°,
∴∠MNE=∠FEQ,
又∵∠QFE=∠MEN=90°,
∴△EFQ∽△NEM,
∴
 =
= ②,
②,由①、②知:
 =
= .
.分析:(1)可将抛物线的解析式设为顶点式,然后将A点坐标代入,即可求得抛物线的解析式;
(2)根据两对相似三角形:△AQF、△ABE和△BGQ、△BDA得出的对应成比例线段,即可求出所求的代数式是否为定值;
(3)易证得△EMN∽△FQE,得
 ①,下面证
①,下面证 ,需通过构建相似三角形求解;
,需通过构建相似三角形求解;过Q作QP⊥BE于P,则四边形FQPE是矩形,FE=QP②;已知E在AB的垂直平分线上,可得:△AEB是等腰Rt△,进一步可知△AFQ、△QEB也是等腰Rt△;易证得△FAQ∽△PQB,得
 ③,联立①②③即可证得所求的结论.
③,联立①②③即可证得所求的结论.点评:此题考查了二次函数解析式的确定、相似三角形的判定和性质、二次函数的性质、等腰直角三角形的判定和性质等知识;(3)题中,能够正确的根据已知和所求条件构建出相似三角形是解题的关键.

练习册系列答案
相关题目
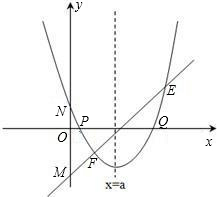 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.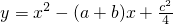 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.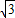 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.