题目内容
如图甲所示,将长为30cm,宽为2cm的长方形白纸条,折成图乙所示的图形并在其一面着色,则着色部分的面积为


| A.60cm2 | B.58 cm2 | C.56 cm2 | D.54 cm2 |
C
考点:
分析:根据折叠的性质,已知图形的折叠就是已知两个图形全等.由图知,着色部分的面积是原来的纸条面积减去两个等腰直角三角形的面积.
解答:解:着色部分的面积=原来的纸条面积-两个等腰直角三角形的面积=30×2-2/2×2×2=56cm2.
故选C.
点评:本题考查图形的折叠变化及等腰直角三角形的面积公式.关键是要理解折叠是一种对称变换.
分析:根据折叠的性质,已知图形的折叠就是已知两个图形全等.由图知,着色部分的面积是原来的纸条面积减去两个等腰直角三角形的面积.
解答:解:着色部分的面积=原来的纸条面积-两个等腰直角三角形的面积=30×2-2/2×2×2=56cm2.
故选C.
点评:本题考查图形的折叠变化及等腰直角三角形的面积公式.关键是要理解折叠是一种对称变换.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)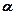 (
(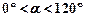 且
且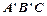 ,
,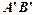 边经过点B时,求旋转角
边经过点B时,求旋转角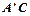 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥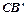 边于点E,联结BE.
边于点E,联结BE.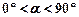 时,设
时,设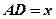 ,
,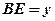 ,求
,求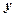 与
与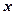 之间的函数解析式及定义域;
之间的函数解析式及定义域;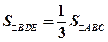 时,求
时,求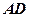 的长.
的长. 

 1至8标明.
1至8标明.
 ,则这个正多边形的边数是________.
,则这个正多边形的边数是________.
