题目内容
 (2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y=
(2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y=| k |
| x |
(1)求k的值;
(2)以原点O为位似中心,将正方形OABC放大,使变换后的正方形OMQN与正方形OABC对应的比为2:1,且正方形OMQN在第一象限内与函数y=
| k |
| x |
分析:(1)由于四边形OABC是面积为4的正方形,易求其边长,从而易知点B的坐标,而点B在反比例函数上,代入可求k;
(2)根据两个正方形的位似比是2:1,易求正方形OMQN的边长,进而可知点E的横坐标、F的纵坐标都是4,而点E、F在反比例函数图象上,代入可分别求出点E、F的坐标,先设所求抛物线的解析式是y=ax2+bx+c,再把点EFB的坐标代入,可得关于a、b、c的三元一次方程组,解可求a、b、c的值,进而可得抛物线的解析式.
(2)根据两个正方形的位似比是2:1,易求正方形OMQN的边长,进而可知点E的横坐标、F的纵坐标都是4,而点E、F在反比例函数图象上,代入可分别求出点E、F的坐标,先设所求抛物线的解析式是y=ax2+bx+c,再把点EFB的坐标代入,可得关于a、b、c的三元一次方程组,解可求a、b、c的值,进而可得抛物线的解析式.
解答:解:(1)∵四边形OABC是面积为4的正方形,
∴OA=AB=2,
∴点B的坐标是(2,2),
又∵点B在y=
上,
∴k=4;
(2)∵OM:OA=2:1,OA=2,
四边形OMQN是正方形,
∴OM=QM=4,
∴点E的横坐标是4,点F的纵坐标是4,
∵点E、F在反比例函数上,
∴点E坐标是(4,1),点F的坐标是(1,4),
设所求抛物线的解析式是y=ax2+bx+c,
把(2,2)、(1,4)、(4,1)代入抛物线解析式,可得
,
解得
,
∴所求抛物线的解析式是y=
x2-
x+7.
∴OA=AB=2,

∴点B的坐标是(2,2),
又∵点B在y=
| k |
| x |
∴k=4;
(2)∵OM:OA=2:1,OA=2,
四边形OMQN是正方形,
∴OM=QM=4,
∴点E的横坐标是4,点F的纵坐标是4,
∵点E、F在反比例函数上,
∴点E坐标是(4,1),点F的坐标是(1,4),
设所求抛物线的解析式是y=ax2+bx+c,
把(2,2)、(1,4)、(4,1)代入抛物线解析式,可得
|
解得
|
∴所求抛物线的解析式是y=
| 1 |
| 2 |
| 7 |
| 2 |
点评:本题时反比例函数综合题,解题的关键是掌握点和函数解析式的关系,会使用待定系数法求函数解析式,以及正方形的性质.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
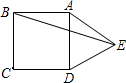 (2012•吴中区一模)如图,在正方形ABCD的外侧作等边△ADE,则∠AEB的度数为( )
(2012•吴中区一模)如图,在正方形ABCD的外侧作等边△ADE,则∠AEB的度数为( ) (2012•吴中区一模)已知集合B中的数与集合A中对应的数之间的关系是某个一次函数,若用y表示集合B中的数,用x表示集合A中的数,求y与x之间的函数关系式,并在集合B中写出与集合A中-2,-1,2,3对应的数值.
(2012•吴中区一模)已知集合B中的数与集合A中对应的数之间的关系是某个一次函数,若用y表示集合B中的数,用x表示集合A中的数,求y与x之间的函数关系式,并在集合B中写出与集合A中-2,-1,2,3对应的数值.