Question

求下列二次函数的图象与x轴的交点坐标，并作草图验证．
（1）y=x²-2x；
（2）y=x²-2x-3．

Answer 1

解：（1）令y=0，则x²-2x=x（x-2）=0，
解得，x=0或x=2，
即抛物线与x轴的交点坐标分别是（0，0），（2，0）．
顶点坐标是（1，1），抛物线开口方向向上
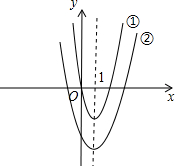
其图象如图①所示；

（2）令y=0，则x²-2x-3=（x-3）（x+1）=0，
解得，x=3或x=-1，
即抛物线与x轴的交点坐标是（3，0），（-1，0）．
令x=0，则y=-3，
即抛物线与y轴的交点坐标是（0，-3），
顶点坐标是（1，-4），抛物线开口方向向上，
其图象如图②所示．
分析：（1）令y=0，通过提取公因式x对方程的左边进行因式分解，利用因式分解法解方程；
（2）令y=0，利用“十字相乘法”的方程的左边进行因式分解，然后解方程．
根据抛物线与坐标轴的交点化草图．
点评：本题考查了抛物线与x轴的交点．画抛物线时，需要抛物线与坐标轴的交点坐标，开口方向，顶点坐标．