题目内容

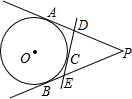精英家教网如图所示，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是
AB
上任意一点，过C作⊙O的切线分别交PA，PB于D，E．若△PDE的周长为12，则PA的长为（　　）
A、12B、6C、8D、4
分析：由PA，PB分别和⊙O切于A，B两点与DE是⊙O的切线，根据切线长定理，即可得PA=PB，DA=DC，EB=EC，又由△PDE的周长为12，易求得PA+PB=12，则可求得答案．
解答：解：∵PA，PB分别和⊙O切于A，B两点，
∴PA=PB，
∵DE是⊙O的切线，
∴DA=DC，EB=EC，
∵△PDE的周长为12，
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12，
∴PA=6．
故选B．
点评：此题考查了切线长定理．此题难度不大，解题的关键是熟练应用切线长定理，注意数形结合思想与整体思想的应用．
练习册系列答案
相关题目
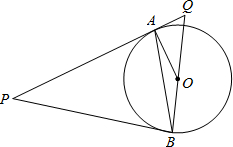如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA精英家教网=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．
（1）求证：PB是⊙O的切线；
（2）求证：AQ•PQ=OQ•BQ；
（3）设∠AOQ=α，若cosα=
45
，OQ=15，求AB的长．
如图所示，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是
AB
上任意一点，过C作⊙O的切线分别交PA，PB于D，E．
（1）若△PDE的周长为10，则PA的长为
5
5
；
（2）连接CA、CB，若∠P=50°，则∠BCA的度数为
115
115
度．

如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．

（1）求证：PB是⊙O的切线；
（2）求证：AQ•PQ=OQ•BQ；
（3）设∠AOQ=α，若cosα= ，OQ=15，求AB的长．
[来源:学科网ZXXK]

如图所示．P是⊙O外一点．PA是⊙O的切线．A是切点．B是⊙O上一点．且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．

（1）求证：PB是⊙O的切线；
（2）求证： AQ?PQ= OQ?BQ； 
（3）设∠AOQ=．若cos=．OQ= 15．求AB的长

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网