题目内容
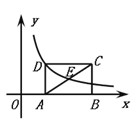
【题目】如图，矩形ABCD中，E是AC的中点，点A、B在x轴上．若函数
（
）的图像过D、E两点，则矩形ABCD的面积为______．
【答案】16
【解析】分析：过E作EF⊥AB于F，由三角形中位线定理可得AD=2EF，设点D的横坐标为m，D点坐标为（m，
），得出AD=
，即可得出EF=
，根据图象上的坐标特征得出E的横坐标为2m，继而得出AB=2m，然后根据矩形的面积公式即可求得．
详解：过E作EF⊥AB于F，
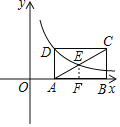
∵点E是矩形ABCD对角线的交点，
∴AE=CE，
∴EF是△ABC的中位线，
∴AD=2EF，
设点D的横坐标为m，且点D在反比例函数y=（x＞0）上，
∴D点坐标为（m，），
∴AD=，
∴EF=，
∴E（2m，），
∴AF=m，
∴AB=2m，
∴矩形ABCD的面积=2m=16，
故答案为16．
练习册系列答案
相关题目
【题目】某商场欲购进果汁饮料和碳酸饮料共60箱，两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注：总利润＝总售价－总进价）。
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数解析式；
（2）求总利润w关于x的函数解析式；
（3）如果购进两种饮料的总费用不超过2100元，那么该商场如何进货才能获利最多？并求出最大利润。
饮料 | 果汁饮料 | 碳酸饮料 |
进价（元/箱） | 40 | 25 |
售价（元/箱） | 52 | 32 |
【题目】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数：
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数．
(2)假如生产部负责人把每位工人的月加工零件个数定为260，你认为这个定额是否合理？为什么？
