Question

（1）计算：(

3

)2+4×(-

1

2

)-23；
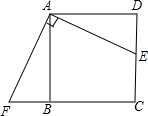
（2）已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF．求证：DE=BF．

Answer 1

分析：（1）按有理数的运算法则计算即可；
（2）由同角的余角相等知，∠FAB=∠DAE，由正方形的性质知，∠AB=AD，∠ABF=∠ADE=90°，则ASA证得△AFB≌△ADE?DE=BF．

解答：（1）解：原式=3-2-8=-7；

（2）证明：∵∠FAB+∠BAE=90°，∠DAE+∠BAE=90°，
∴∠FAB=∠DAE，
∵∠AB=AD，∠ABF=∠ADE，
∴△AFB≌△ADE，
∴DE=BF．

点评：此题即考查了实数的运算又考查了正方形的性质．学生对学过的知识要系统起来．