ΧβΡΩΡΎ»ί
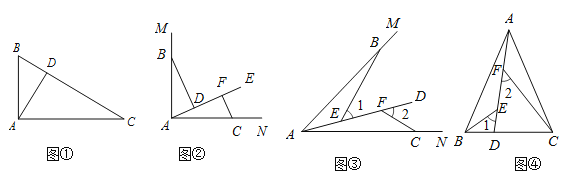
ΓΨΧβΡΩΓΩΈ Χβ«ιΨ≥ΘΚ»γΆΦΔΌΘ§‘Ύ÷±Ϋ«»ΐΫ«–ΈABC÷–Θ§ΓœBAC=![]() Θ§ADΓΆBC”ΎΒψD,Ω…÷ΣΘΚΓœBAD=ΓœCΘ®≤Μ–η“Σ÷ΛΟςΘ©ΘΜ
Θ§ADΓΆBC”ΎΒψD,Ω…÷ΣΘΚΓœBAD=ΓœCΘ®≤Μ–η“Σ÷ΛΟςΘ©ΘΜ
Θ®1Θ©ΧΊάΐΧΫΨΩΘΚ»γΆΦΔΎΘ§ΓœMAN=90ΓψΘ§…δœΏAE‘Ύ’βΗωΫ«ΒΡΡΎ≤ΩΘ§ΒψBΓΔC‘ΎΓœMANΒΡ±ΏAMΓΔAN…œΘ§«“AB=AC, CFΓΆAE”ΎΒψF,BDΓΆAE”ΎΒψD.÷ΛΟςΘΚΓςABDΓ’ΓςCAF;
Θ®2Θ©ΙιΡ…÷ΛΟςΘΚ»γΆΦΔέΘ§ΒψBΘ§C‘ΎΓœMANΒΡ±ΏAMΓΔAN…œΘ§ΒψEΘ§F‘ΎΓœMANΡΎ≤ΩΒΡ…δœΏAD…œΘ§Γœ1ΓΔΓœ2Ζ÷±π «ΓςABEΓΔΓςCAFΒΡΆβΫ«.“―÷ΣAB=AC,Γœ1=Γœ2=ΓœBAC. «σ÷ΛΘΚΓςABEΓ’ΓςCAF;
Θ®3Θ©ΆΊ’Ι”Π”ΟΘΚ»γΆΦΔήΘ§‘ΎΓςABC÷–Θ§AB=ACΘ§ABΘΨBC.ΒψD‘Ύ±ΏBC…œΘ§CD=2BDΘ§ΒψEΓΔF‘ΎœΏΕΈAD…œΘ§Γœ1=Γœ2=ΓœBAC.»τΓςABCΒΡΟφΜΐΈΣ15Θ§‘ρΓςACF”κΓςBDEΒΡΟφΜΐ÷°ΚΆΈΣ .
ΓΨ¥πΑΗΓΩ(1)ΓΔ÷ΛΟςΙΐ≥ΧΦϊΫβΈωΘΜ(2)ΓΔ÷ΛΟςΙΐ≥ΧΦϊΫβΈωΘΜ(3)ΓΔ5.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚ(1)ΓΔΗυΨί¥Ι÷±ΒΟ≥ωΓœBDA=ΓœAFC =90ΓψΘ§»ΜΚσΗυΨίΥΪ¥Ι÷±ΒΟ≥ωΓœABD=ΓœCAFΘ§¥”ΕχΥΒΟςΓςABDΓςCAF»ΪΒ»ΘΜ(2)ΓΔΗυΨίΓœ1ΘΫΓœBACΘ§Γœ1=ΓœBAE+ΓœABEΘ§ΓœBAC=ΓœBAE+ΓœCAFΒΟ≥ωΓœABE=ΓœCAFΘ§»ΜΚσΆ§άμΒΟ≥ωΓœBAE=ΓœFCAΘ§¥”ΕχΒΟ≥ω»ΐΫ«–Έ»ΪΒ»ΘΜ(3)ΓΔΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΈ ΧβΒΟ≥ω¥πΑΗ.
‘ΧβΫβΈωΘΚ(1)ΓΔ»γΆΦΔΎ ΓΏCFΓΆAE, BDΓΆAE, ΓœMAN=900 ΓύΓœBDA=ΓœAFC =90o
ΓύΓœABD+ΓœBAD=90o ΓΏΓœBAD+ΓœCAF=90o ΓύΓœABD=ΓœCAF
Γύ‘ΎΓςABDΚΆΓςCAF÷–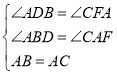 ΓςABDΓ’ΓςCAF(AAS)
ΓςABDΓ’ΓςCAF(AAS)
(2)ΓΔ»γΆΦΔέ ΓΏΓœ1ΘΫΓœBAC, Γœ1=ΓœBAE+ΓœABE. ΓœBAC=ΓœBAE+ΓœCAF.
ΓύΓœABE=ΓœCAFΆ§άμΒΟ ΓœBAE=ΓœFCA .
‘ΎΓςABEΚΆΓςCAF÷–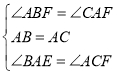 ΓύΓςABEΓ’ΓςCAF(ASA) \
ΓύΓςABEΓ’ΓςCAF(ASA) \
(5)ΓΔ5

ΓΨΧβΡΩΓΩ‘Ύ“Μ¥Έ÷–―ß…ζΧοΨΕ‘ΥΕ·Μα…œΘ§≤ΈΦ”Ρ–Ή”ΧχΗΏΒΡ15Οϊ‘ΥΕ·‘±ΒΡ≥…Φ®»γœ¬±μΥυ ΨΘΚ
≥…Φ®/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
»Υ ΐ | 2 | 3 | 2 | 3 | 4 | 1 |
‘ρ’β–©‘ΥΕ·‘±≥…Φ®ΒΡ÷–ΈΜ ΐΓΔ÷Ύ ΐΖ÷±πΈΣ( )
A. 1.70Θ§1.75 B. 1.70Θ§1.70
C. 1.65Θ§1.75 D. 1.65Θ§1.70