题目内容
【题目】在下列说法中,正确的是( )
A.如果两个三角形全等,则它们必是关于直线成轴对称的图形
B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形
C.等腰三角形是关于底边中线成轴对称的图形
D.一条线段是关于经过该线段中点的直线成轴对称的图形
【答案】B
【解析】
试题解析:解:A选项:全等三角形不一定是轴对称图形,故A选项错误;
B选项:如果两个三角形关于某直线成轴对称,则这两个三角形一定可以完全重合,所以它们是全等三角形,故B选项正确;
C选项:等腰三角形的对称轴是等腰三角形底边中线所在的直线,故B选项错误;
D选项:线段的对称轴是线段的垂直平分线,经过线段中点的直线有无数条,故D选项错误.
故应选B.

练习册系列答案
相关题目
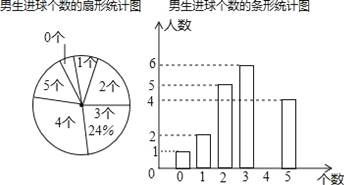
【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.