题目内容
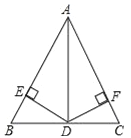
【题目】如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．
（1）求证：AB=AC；
（2）若AD=
，∠DAC=30°，求AC的长．
【答案】（1）证明见解析；（2）4．
【解析】
试题分析：（1）先证明△DEB≌△DFC得∠B=∠C由此即可证明．
（2）先证明AD⊥BC，再在RT△ADC中，利用30°角性质设CD=a，AC=2a，根据勾股定理列出方程即可解决问题．
试题解析：（1）证明：∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，∴DE=DF，∠DEB=∠DFC=90°，在RT△DEB和RT△DFC中，∵BD=DC，DE=DF，∴△DEB≌△DFC，∴∠B=∠C，∴AB=AC．
（2）∵AB=AC，BD=DC，∴AD⊥BC，在RT△ADC中，∵∠ADC=90°，AD=
，∠DAC=30°，∴AC=2CD，设CD=a，则AC=2a，∵
，∴
，∵a＞0，∴a=2，∴AC=2a=4．
练习册系列答案
相关题目
【题目】随着车辆的增加，交通违规的现象越来越严重，交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理（速度在30﹣40含起点值30，不含终点值40），得到其频数及频率如表：
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | c |
50﹣60 | a | 0.39 |
60﹣70 | b | d |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
（1）表中a、b、c、d分别为：a=； b=； c=； d= ．
（2）补全频数分布直方图；
（3）如果某天该路段约有1500辆通过，汽车时速不低于60千米即为违章，通过该统计数据估计当天违章车辆约有多少辆？ 
