Question

（2012•宁津县二模）如图所示，我班同学组织课外实践活动，预测量一建筑物的高度，在建筑物附近一斜坡A点测得建筑物顶端D的仰角为30°，在坡底C点测得建筑物顶端D的仰角为60°，已知A点的高度AB为20米，AC的坡度为1：1（即AB：BC=1：1），且B、C、E三点在同一条直线上，请根据以上条件求出建筑物DE的高度（测量器的高度忽略不计）．

Answer 1

分析：根据矩形性质得出AF=BE，EF=AB=20，再利用锐角三角函数的性质求出CE=

3

3

x，再利用DF=AF•tan30°，DE=DF+FE求出DE的长即可．

解答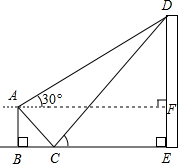：解：如图，过点A作AF⊥DE于F，
则四边形ABEF为矩形．
故AF=BE，EF=AB=20．
设 DE为x，
在直角三角形CDE中，CE=

DE

tan∠DCE

=

DE

tan60°

=

3

3

x，
在直角三角形ABC中，BC=AB=20，
在直角三角形AFD中，∵DF=AF•tan30°=

3

3

（BC+CE）=

3

3

（20+

3

3

x），
∴DE=DF+FE=

3

3

（20+

3

3

x）+20=x，
解方程得：x=30+10

3

（米），
答：建筑物的高度为30+10

3

米．

点评：此题主要考查了解直角三角形的应用以及坡度的定义，根据锐角三角函数的关系得出DF的长是解题关键．